
En entregas anteriores, hemos explorado diversas métricas de centralidad que permiten identificar los nodos más relevantes dentro de una red. En esta ocasión, nos centraremos en la centralidad de Katz, una medida que extiende el concepto de centralidad de autovector al considerar no solo las conexiones directas de un nodo, sino también aquellas indirectas, a través de caminos más largos, ponderados según su distancia.
La centralidad de Katz resulta especialmente útil en redes donde la influencia no se limita únicamente a los vínculos inmediatos, sino que se difunde progresivamente a través de múltiples intermediarios. Este es el caso de estructuras complejas como las redes sociales, los sistemas de transporte o los modelos de propagación de información, donde el impacto de un nodo puede extenderse más allá de su vecindario directo.
A diferencia de la centralidad de grado, que simplemente cuenta el número de conexiones de un nodo, la centralidad de Katz incorpora un factor de atenuación que reduce progresivamente la influencia de los nodos más alejados. Esta característica permite identificar con mayor precisión los nodos verdaderamente influyentes, incluso cuando estos tienen una cantidad similar de enlaces que otros menos relevantes.
En contextos donde la conectividad global es más significativa que las relaciones individuales —como en el análisis de estrategias de marketing viral, la vigilancia epidemiológica o la difusión de ideas en redes sociales— la centralidad de Katz proporciona una herramienta para modelar la dinámica de la influencia dentro del grafo.

Interpretación de la centralidad de Katz
La fórmula de la centralidad de Katz se basa en una extensión del concepto de centralidad de autovector, incorporando un término adicional que permite que todos los nodos tengan una centralidad no nula, incluso si no están directamente conectados a nodos altamente influyentes.
Formalmente, la centralidad de Katz para un nodo i se define como: C_{Katz}(i) = \alpha \sum_{j=1}^{n} A_{ij} x_j + \beta, donde:
- A_{ij} es la matriz de adyacencia del grafo.
- \alpha es el factor de atenuación (también llamado parámetro de decaimiento), que debe ser suficientemente pequeño para garantizar la convergencia.
- \beta es una constante positiva que representa la contribución exógena a la centralidad de cada nodo (puede ser un escalar o un vector).
La elección del parámetro \alpha es crucial: debe ser menor que el inverso del mayor valor propio (autovalor) de la matriz de adyacencia, para garantizar la convergencia de la solución. Es decir, \alpha < 1/\lambda_1 donde \lambda_1 es el mayor autovalor de la matriz de adyacencia.
Esta fórmula puede interpretarse como una serie geométrica de caminos ponderados, donde las contribuciones de los vecinos más lejanos se atenúan progresivamente a medida que aumenta la longitud del camino.
Aplicaciones de la centralidad de Katz
Esta métrica es de especial utilidad cuando la influencia se propaga más allá de los enlaces directos. Algunas de sus aplicaciones más destacadas incluyen:
- Redes sociales: Identificación de personas con gran capacidad de influencia, incluso si no tienen muchas conexiones directas.
- Sistemas de recomendación: Medición del impacto potencial de usuarios o productos en redes de comportamiento o preferencias.
- Redes de transporte: Evaluación de la importancia estructural de estaciones o rutas considerando rutas indirectas.
- Ciencias biomédicas: Análisis de redes de interacción de proteínas o de propagación de enfermedades.
- Motores de búsqueda y SEO: Valoración de páginas web en función de enlaces directos e indirectos (con conceptos relacionados como PageRank).
- Estabilidad financiera: Detección de entidades con impacto sistémico en redes de crédito o flujo de capital.
Implementación de la centralidad de Katz en igraph
En R, la centralidad de Katz se puede calcular utilizando la función alpha_centrality() del paquete igraph. Aunque el nombre pueda inducir a pensar que se trata de otra métrica, esta función implementa efectivamente el cálculo de la centralidad de Katz, al permitir especificar un parámetro de atenuación alpha y un vector exógeno exo (que representa el valor base o contribución externa de cada nodo).
Veamos cómo implementarla con un ejemplo sencillo:
# Cargar el paquete igraph library(igraph) # Crear un grafo no dirigido g <- graph(edges = c(1,2, 1,3, 2,4, 2,5, 3,6, 5,6, 4,5, 3,4), directed = FALSE) # Calcular la centralidad de Katz usando alpha_centrality # alpha: factor de atenuación # exo: valor exógeno (contribución base), se puede dejar en 1 # tol: tolerancia para la convergencia del algoritmo iterativo centralidad_katz <- alpha_centrality(g, alpha = 0.1, exo = 1, tol = 1e-7) # Asignar los valores de centralidad a los nodos V(g)$katz <- round(centralidad_katz, 3) # Mostrar los valores de centralidad por nodo centralidad_katz
Este código devuelve un vector con la centralidad de Katz de cada nodo en la red. Los valores que se obtiene son:
1.280987 1.411458 1.398411 1.422133 1.411458 1.280987
En este punto es importante tener en cuenta el significado de los diferentes parámetros que se ha usado en el cálculo:
alpha: controla cuánto se atenúa la influencia de nodos más alejados. Valores pequeños (e.g., 0.1) aseguran que las contribuciones lejanas disminuyen rápidamente. Si es demasiado grande, el cálculo puede no converger.exo: representa una contribución externa constante a cada nodo. Por defecto puede usarse1.tol: nivel de tolerancia para determinar la convergencia.
Visualización del grafo con valores de Katz
Para interpretar mejor los resultados, podemos representar el grafo y mostrar el valor de centralidad de Katz directamente en cada nodo:
plot(g,
vertex.label = V(g)$katz,
vertex.size = 30,
main = "Centralidad de Katz en un grafo simple")Lo que produce una gráfica como la que se muestra a continuación en donde se muestra la centralidad de Katz en cada uno de los nodos.
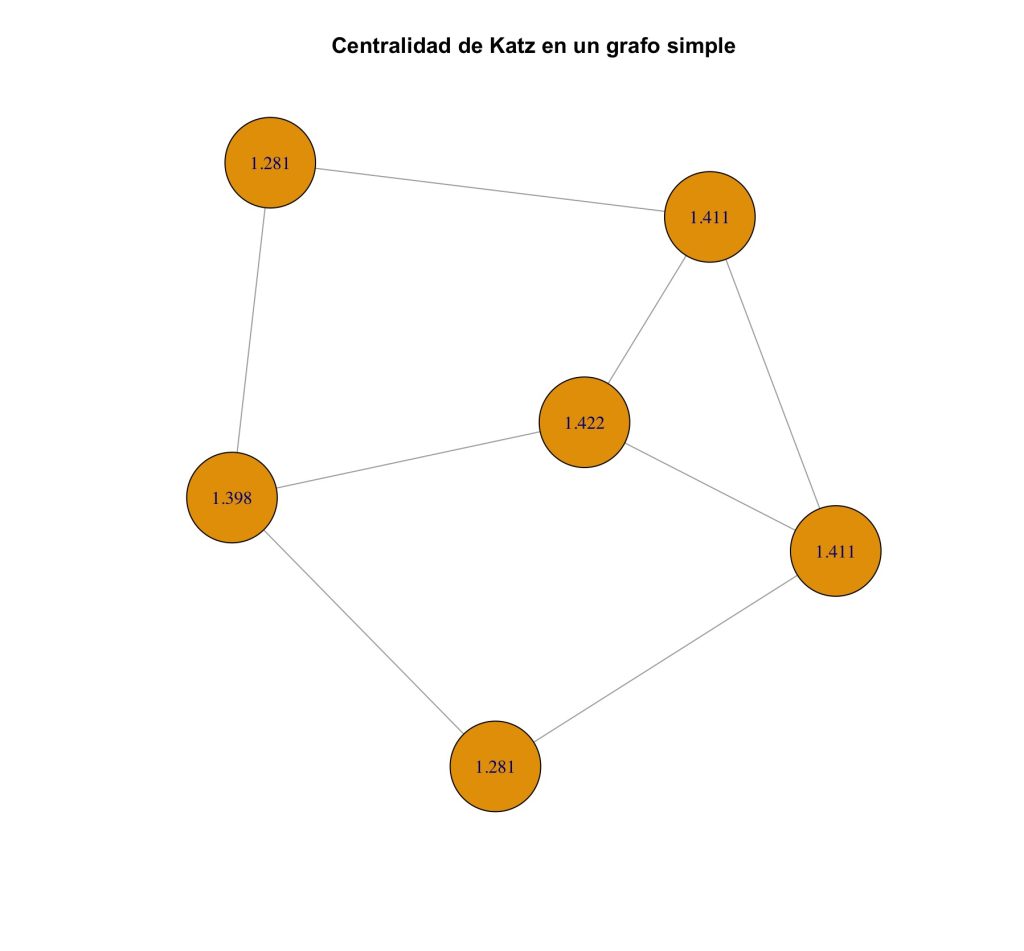
Interpretación de los resultados
La centralidad de Katz proporciona una medida de la influencia de cada nodo, tomando en cuenta tanto sus conexiones directas como las indirectas. A continuación, explico cómo interpretar los resultados obtenidos:
- Nodos con alta centralidad de Katz: Estos nodos no solo tienen conexiones directas con otros nodos importantes, sino que también están bien conectados indirectamente. Es decir, tienen influencia no solo por su cantidad de conexiones, sino por las conexiones de los nodos a los que están conectados.
- Nodos con baja centralidad de Katz: Estos nodos son menos influyentes en la red, ya que, aunque puedan tener algunos enlaces, su influencia es limitada por su falta de conexión indirecta con otros nodos clave.
En el caso de nuestro ejemplo, la centralidad de Katz tiene en cuenta que los nodos no solo dependen de sus conexiones inmediatas, sino también de los caminos indirectos a través de otros nodos. Si un nodo está conectado a muchos otros nodos clave, su centralidad de Katz será más alta.
Conclusiones
La centralidad de Katz es una métrica para evaluar la importancia de los nodos en una red, considerando tanto las conexiones directas como las indirectas. Su flexibilidad hace que sea aplicable en una amplia gama de problemas, desde la clasificación de páginas web hasta el análisis de redes sociales y sistemas de transporte. Además, permite una interpretación más realista de la influencia en redes complejas.
En la próxima entrega, abordaremos la centralidad de Bonacich, que extiende el concepto de la centralidad de Katz con un enfoque en la dependencia y poder relacional en redes sociales y económicas.
Nota: La imagen de este artículo fue generada utilizando un modelo de inteligencia artificial.
Deja una respuesta