Los histogramas son una herramienta fantástica para visualizar la frecuencia de los diferentes valores de un conjunto de datos. Permitiendo ver rápidamente la distribución de la población. Lo que se hace dividiendo el rango del conjunto de datos en grupos de la misma anchura, a los que se suelen denominar bins, y contar el número de valores que caen en cada uno de estos. Siendo este número de bins clave para poder ver correctamente la distribución de los datos. Usar un número demasiado bajo de bins hará que no se pueda apreciar la distribución en la figura, mientras que emplear un número demasiado alto solamente se verá ruido. Para ello saber como obtener el número óptimo de bins para un histograma es clave.
Tabla de contenidos
El problema del número de bins en un histograma
En primer lugar, es adecuado ver el problema que representa no usar el número adecuado de bins en un histograma. Para ello se puede crear un conjunto de datos aleatorios con una distribución normal, en la que un porcentaje de los datos se desplaza un valor dado. Lo que nos creará un conjunto de datos bimodal. Forma que se puede ver fácilmente con un histograma.
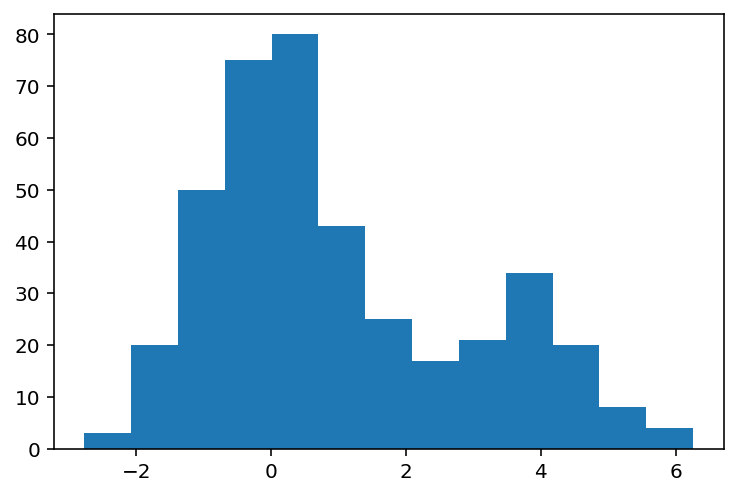
import numpy as np from matplotlib.pyplot import hist data = np.random.RandomState(0).randn(400) data[300:] += 4 hist(data, bins='auto')

En este ejemplo se le ha indicado a la función hist() que determine automáticamente el número de bins con la opción 'auto' del parámetro bins. Seleccionando en este caso 13 que con los que se puede ver fácilmente la forma de la distribución. Ahora, si se crea un histograma solamente con 3 bins, las conclusiones que se podrían sacar de esta figura no serían correctas.


Los mismo en el caso de usar demasiados bins, por ejemplo 100.

Reglas para calcular el número óptimo de bins para un histograma
Generalmente la función hist() de Matplotlib calcula de una forma correcta el número óptimo de bins para el conjunto de datos usado. Aunque en algunos casos puede ser necesario saber cómo calcular este. Para lo que se pueden usar, entre otras, dos reglas: Sturges y Freedman–Diaconis.
La regla de Sturges
Para la obtención de la regla de Sturges solamente se tiene que asumir que el número de muestras en cada intervalo de un histograma ideal viene dado por el coeficiente binomial. Así el número total de muestras se puede obtener sumando el de cada uno de los intervalos.
N = \sum_{i=0}^{k-1} \binom{k-1}{i} = 2^{k-1}Por lo que se puede obtener una fórmula que depende únicamente de la cantidad de valores que existen en el conjunto de datos.
k_{Sturges} = \log_2|n| + 1La regla de Freedman–Diaconis
En el caso de la regla de Freedman–Diaconis se usa un enfoque diferente al anterior. Buscando identificar el ancho de los bins de tal manera que se minimice la diferencia entre la integral de histograma y la función de distribución teórica. Para lo que se usa la siguiente expresión
width_{FD} = 2 \frac{IRQ}{\sqrt[3]{n}}Donde IRQ representa el rango intercuartílico y n el número de valores del conjunto de datos.
Selección de una regla
En la mayoría de los casos el número de bins que se obtendrá usando las reglas anteriores será diferente. Por lo que una buena opción es calcular ambos y quedarnos con el mayor de los dos valores. Siendo esta la opción que se implementa en muchas librerías.
Implementación en Python de las reglas
Ahora que conocemos las dos reglas se pueden implementar en Python para comprobar que el número óptimo de bins en nuestro ejemplo es el que ha seleccionado la función hist().
def sturges(data):
num_data = len(data)
num_bins = np.int(np.log2(num_data)) + 1
return num_bins
def freedman_diaconis(data):
num_data = len(data)
irq = np.percentile(data, 75) - np.percentile(data, 25)
bin_width = 2 * irq / np.power(num_data, 1/3)
num_bins = np.int((np.max(data) - np.min(data)) / bin_width) + 1
return num_binsAl usar ambas funciones se puede ver que la regla de Sturges indica que el valor óptimo es 9, mientras que la regla de Freedman–Diaconis indica 13. Siendo este último, el máximo de los dos, el que previamente había calculado la función hist().
Conclusiones
En esta ocasión se han visto dos reglas que se pueden emplear para calcular el número óptimo de bins para un histograma.
Deja una respuesta