
En el análisis de redes, identificar los nodos más influyentes es clave para comprender cómo se organiza y se comporta un sistema. Uno de los algoritmos más importantes en este ámbito es PageRank, desarrollado originalmente por Larry Page y Sergey Brin en 1998. Este algoritmo sería la base del motor de búsqueda de Google, revolucionando la forma en que se clasifican las páginas web.
A diferencia de otras métricas más simples, como la centralidad de grado, que solo cuenta la cantidad de enlaces que recibe un nodo, PageRank tiene en cuenta también la importancia de quienes enlazan a dicho nodo. Es decir, no todos los enlaces valen lo mismo: recibir un enlace desde un nodo influyente cuenta más que recibirlo de uno poco conectado.
Esta lógica lo hace especialmente útil no solo para motores de búsqueda, sino también en otras áreas como:
- Biología: para analizar redes de interacción entre proteínas.
- Economía: para estudiar los flujos de comercio entre países o empresas.
- Sociología: para identificar personas influyentes en redes sociales.
- Sistemas de recomendación: como una forma de evaluar la relevancia de productos o contenidos.
En esta entrada, explicaremos en detalle el algoritmo PageRank, sus diferencias con la centralidad de autovector, y como implementar en R con igraph.
Tabla de contenidos
¿Qué es PageRank?
PageRank es un algoritmo que asigna un puntaje de importancia a cada nodo de una red dirigida. Su filosofía se resume en una idea sencilla: “una página es importante si otras páginas importantes la enlazan”. La clave está en que esos enlaces también están ponderados: un enlace desde un nodo relevante cuenta más que uno desde un nodo periférico.

Formulación matemática de PageRank
Supongamos una red dirigida con n nodos. Podemos representarla mediante una matriz de adyacencia A, donde A_{ij} = 1 si existe un enlace del nodo j hacia el nodo i (invertido la conexión porque se desea saber quién recibe el enlace), y 0 en caso contrario.
PageRank define la puntuación para cada uno de los nodos mediante la siguiente expresión: PR(i) = \alpha \sum_{j \in B_i} \frac{PR(j)}{L(j)} + \frac{1 - \alpha}{n} donde:
- PR(i): valor de PageRank del nodo i,
- B_i: conjunto de nodos que enlazan hacia i,
- L(j)[latex]: número de enlaces salientes del nodo [latex]j,
- \alpha: factor de amortiguación o damping factor (generalmente 0,85),
- \frac{1 - \alpha}{n}: probabilidad de "teletransportarse" a un nodo aleatorio.
Este modelo representa el comportamiento de un navegante que sigue enlaces con probabilidad \alpha, pero que con probabilidad 1 - \alpha decide ir a una página cualquiera.
Desde el punto de vista matricial, esta fórmula equivale a encontrar el vector propio principal de una matriz estocástica derivada de la matriz de adyacencia. El valor de PageRank es el vector \mathbf{r} que satisface: \mathbf{r} = \alpha M \mathbf{r} + (1 - \alpha)\mathbf{v} donde:
- M: matriz de transición (normalizada por columnas),
- \mathbf{v}: vector de personalización, usualmente uniforme (\mathbf{v} = \frac{1}{n}).
Este sistema converge iterativamente y garantiza una solución única bajo ciertas condiciones (como que la red sea fuertemente conectada o se utilice el damping).
Diferencias entre PageRank y la centralidad de autovector
Tanto PageRank como la centralidad de autovector (eigenvector centrality) se basan en la intuición de que un nodo es importante si está conectado a otros nodos importantes. Sin embargo, existen diferencias clave entre ambos métodos:
- Direccionalidad:
- La centralidad de autovector puede aplicarse tanto a redes dirigidas como no dirigidas.
- PageRank fue diseñado específicamente para redes dirigidas.
- Propagación de la importancia:
- En la centralidad de autovector, la influencia de los vecinos se transmite directamente, sin ajustar por cuántos enlaces emiten.
- PageRank divide su influencia entre todos los enlaces salientes, es decir, distribuye su importancia.
- Factor de amortiguación (\alpha):
- PageRank introduce este parámetro, que permite modelar la posibilidad de “saltar” a cualquier nodo de forma aleatoria.
- La centralidad de autovector no tiene este mecanismo, por lo que puede presentar problemas de estabilidad en redes muy grandes o dispersas.
- Estabilidad en redes grandes:
- PageRank es más robusto en redes con muchas conexiones y estructuras complejas.
- La centralidad de autovector puede verse afectada por pequeños cambios en la red.
Debido a estas diferencias, PageRank es más estable cuando se trabaja con redes grandes en las que los nodos pueden recibir enlaces de diferentes partes del sistema, como ocurre en la web. En cambio, la centralidad de autovector es más útil en redes donde la influencia está distribuida de manera más uniforme y no depende tanto de un nodo de inicio particular.
En resumen, las diferencias entre ambas métricas se pueden ver en la siguiente tabla
| Métrica | Tipo de red | Considera importancia de enlaces | Factor de amortiguación |
|---|---|---|---|
| Autovector | Dirigidas y no dirigidas | Sí | No |
| PageRank | Dirigidas | Sí | Sí |
Implementación en igraph con page_rank()
Para calcular PageRank en R, utilizamos la librería igraph, que proporciona la función page_rank() para estimar la importancia de cada nodo en una red dirigida. A continuación, presentamos un ejemplo básico y uno aplicado a red web simulada.
Ejemplo básico en R
En primer lugar, creamos un grafo dirigido con seis nodos (A, B, C, D, E, F) y aristas que representan relaciones entre ellos. Luego, aplicamos la función page_rank() para obtener la importancia relativa de cada nodo según su posición en la estructura de la red.
library(igraph)
# Crear un grafo dirigido
g <- graph(edges = c("A", "B", "A", "C", "B", "D", "B", "E", "C", "F", "E", "F", "D", "E", "C", "D"), directed = TRUE)
# Calcular el PageRank con factor de amortiguación de 0.85
pr <- page_rank(g, damping = 0.85)
# Mostrar los valores de PageRank de cada nodo
pr$vectorEn este código:
- Se define un grafo dirigido mediante el vector de aristas.
- Se calcula el PageRank de cada nodo con un factor de amortiguación de 0.85, que representa la probabilidad de seguir un enlace en lugar de saltar aleatoriamente a otro nodo.
- Finalmente, se imprimen los valores obtenidos, que indican la relevancia de cada nodo en la red.
Obteniendo como resultado los siguientes valores:
A B C D E F
0.07084927 0.10096021 0.10096021 0.15666544 0.24692298 0.32364189
Lo que indica que el nodo F es el más importante, seguido del nodo E.
Para interpretar mejor estos resultados, es útil visualizar el grafo, ajustando el tamaño de cada nodo de acuerdo con su valor de PageRank. Esto permite identificar rápidamente los nodos más influyentes visualmente.
# Escalar el tamaño de los nodos según su PageRank
V(g)$size <- pr$vector * 190
# Ajustar el tamaño de las etiquetas y las flechas
V(g)$label.cex <- 1.2
E(g)$arrow.size <- 0.5
# Colorear los nodos según su valor de PageRank
V(g)$color <- heat.colors(length(V(g)))[rank(-pr$vector)]
# Dibujar la red con los valores de PageRank
plot(g,
edge.width = 2,
main = "PageRank en la Red")Aquí:
- Se escala el tamaño de cada nodo proporcionalmente a su valor de PageRank.
- Se utilizan colores cálidos (de
heat.colors) para reflejar visualmente la influencia de cada nodo. - Se ajustan detalles gráficos como el tamaño de las etiquetas y flechas para una visualización más clara.
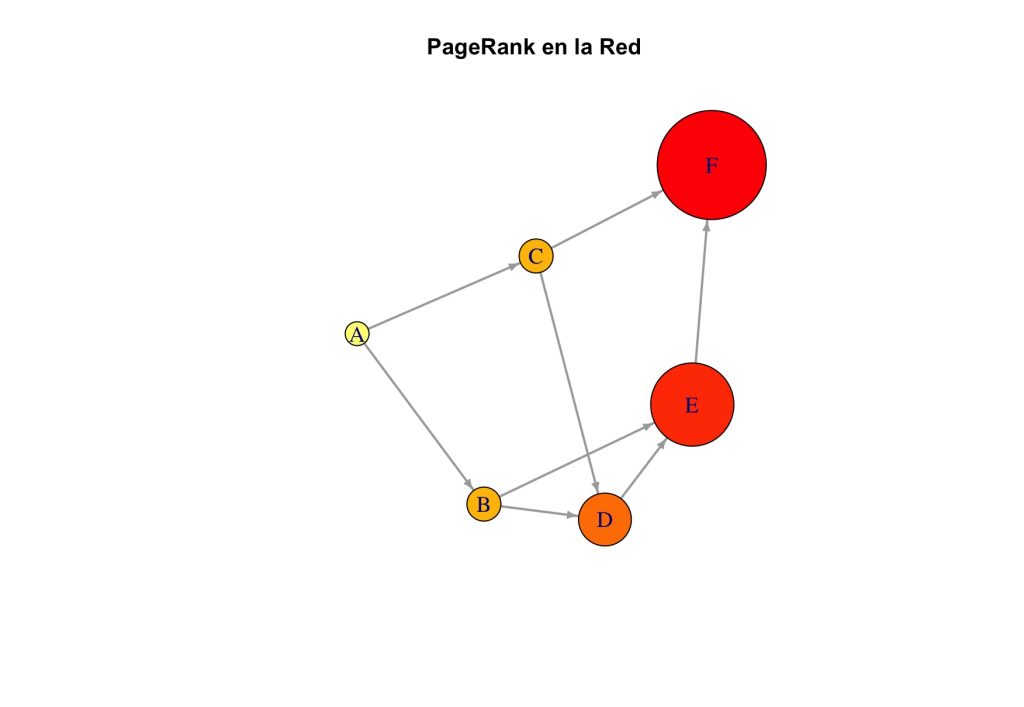
Esta gráfica hace más sencilla la identificación de los nodos más importantes en la red. Por ejemplo, si un nodo tiene muchos enlaces entrantes desde otros nodos importantes, su PageRank será alto y aparecerá más grande y colorido en el grafo. Lo que sucede en el nodo F y en menor grado en el E.
Ejemplo con una red web simulada
Para ilustrar un caso más realista, simulamos una red en la que los nodos representan páginas web y las aristas los enlaces entre ellas.
# Crear una red dirigida donde los nodos representan páginas web
web <- graph(edges = c("Inicio", "Contacto",
"Inicio", "Blog",
"Blog", "Articulo1",
"Blog", "Articulo2",
"Articulo1", "Contacto",
"Articulo2", "Contacto",
"Articulo2", "Inicio"),
directed = TRUE)
# Calcular el PageRank de las páginas web
pr_web <- page_rank(web, damping = 0.85)
# Mostrar los valores de PageRank de cada nodo
pr_web$vectorEn este ejemplo:
- La red está compuesta por nodos como "Inicio", "Blog", "Contacto" y artículos específicos.
- Los enlaces reflejan navegación típica entre secciones de un sitio web.
- Se calcula el PageRank de cada nodo usando el mismo principio que antes.
El resultado indica que el nodo más importante es la página "Contacto”, ya que los resultados son:
Inicio Contacto Blog Articulo1 Articulo2
0.1593625 0.3625498 0.1593625 0.1593625 0.1593625
Visualizamos la red aplicando los mismos criterios de estilo para resaltar la relevancia de cada página:
# Escalar tamaño de nodos según PageRank
V(web)$size <- pr_web$vector * 290
# Ajustes visuales para mejorar la presentación
V(web)$label.cex <- 1.2
E(web)$arrow.size <- 0.5
V(web)$color <- heat.colors(length(V(web)))[rank(-pr_web$vector)]
# Mostrar la red simulada
plot(web,
edge.width = 2,
main = "PageRank en una Red Web Simulada")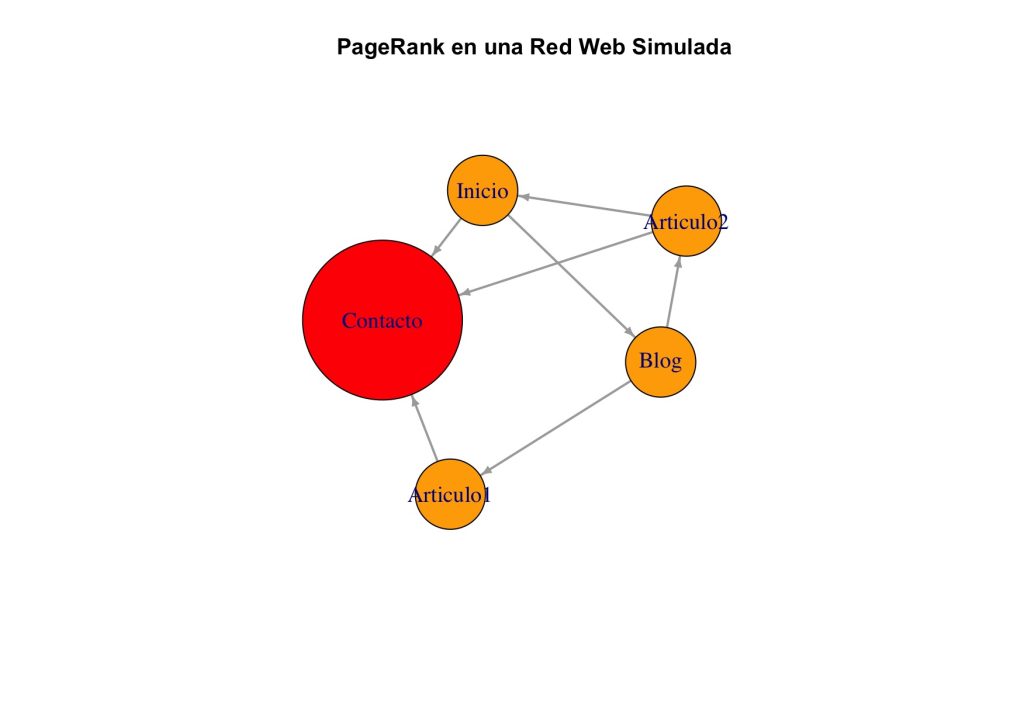
La visualización revela qué páginas web tienen mayor relevancia dentro del sitio. En este caso, "Contacto" tiene un alto PageRank al recibir enlaces desde páginas clave como "Inicio", "Articulo1" y "Articulo2". Esto ilustra cómo PageRank no solo mide la cantidad de enlaces entrantes, sino también su calidad: un enlace desde una página importante vale más que muchos de páginas menos relevantes.
Conclusión
El algoritmo PageRank sigue siendo una herramienta fundamental para evaluar la importancia estructural de los nodos en una red dirigida. Su enfoque va más allá del simple conteo de enlaces entrantes: pondera cada enlace en base a la importancia del nodo emisor, lo que permite capturar la dinámica de influencia acumulada.
En R, su uso mediante la función page_rank() de igraph es sencillo, permitiendo obtener resultados numéricos y visualizaciones intuitivas que hacen más accesible el análisis de redes complejas.
Las aplicaciones de PageRank abarcan desde: Motores de búsqueda (como su uso original en Google), hasta análisis de redes sociales (para identificar usuarios influyentes) o la detección de anomalías en redes de fraude o ciberseguridad.
En la próxima publicación, exploraremos otras métricas clave de centralidad, como la centralidad de autoridad y de prestigio, que complementan a PageRank al captar distintas dimensiones del poder relacional en una red.
Nota: La imagen de este artículo fue generada utilizando un modelo de inteligencia artificial.
Deja una respuesta