Cómo calcular el tamaño de la muestra para encuestas

Calcular adecuadamente el tamaño de la muestra es una parte esencial en el diseño de cualquier encuesta seria. Este paso es fundamental para garantizar que los resultados obtenidos no solo reflejan de forma representativa la realidad de la población, sino que también sean estadísticamente significativos y confiables. Una muestra bien calculada permite optimizar el uso de recursos, logrando resultados válidos con el menor esfuerzo posible. Por el contrario, una muestra mal dimensionada puede producir conclusiones erróneas o inservibles, lo que nos hará perder tanto tiempo como dinero.

En esta entrada, explicaremos los fundamentos teóricos del cálculo del tamaño de muestra, explicaremos los componentes estadísticos clave involucrados y mostraremos cómo aplicar estos conceptos mediante ejemplos prácticos.

Al final de la entrada se mostrará el código Python con el que se puede realizar el cálculo para cualquier condición. No obstante, quienes solo deseen una calculadora pueden ver los resultados directamente en la aplicación de nuestro laboratorio.

¿Qué es el tamaño de la muestra y por qué es tan importante?

El tamaño de la muestra se refiere al número de personas que necesitamos encuestar para que los resultados obtenidos sean estadísticamente válidos y representativos de la población total. Una muestra demasiado pequeña puede llevar a conclusiones erróneas, ya que los datos recogidos tendrán mayor probabilidad de no reflejar adecuadamente las características de la población. Por otro lado, una muestra innecesariamente grande implica un gasto excesivo de tiempo, dinero y esfuerzo, sin que esto suponga una mejora proporcional en la precisión.

En Analytics Lane

¿Está concentrado el MSCI World? Un análisis con Gini, Lorenz y leyes de potencia

La clave está en encontrar un equilibrio adecuado entre precisión estadística y eficiencia operativa. Para lograrlo, es necesario comprender algunos conceptos fundamentales de estadística y aplicar las fórmulas adecuadas que nos permitan determinar cuántas personas deben formar parte de la muestra.

Componentes esenciales del cálculo del tamaño de la muestra

Para calcular el tamaño de la muestra en una encuesta, es necesario entender cuatro conceptos estadísticos clave. La elección de estos elementos es lo que determina el tamaño final de la muestra:

Nivel de confianza (Z)

El nivel de confianza representa el grado de certeza que queremos tener en los resultados de la encuesta. Es decir, indica la probabilidad de que el intervalo de confianza obtenido incluya el verdadero valor poblacional. Los niveles más comunes son:

• 90% (Z = 1,645)
• 95% (Z = 1,96)
• 99% (Z = 2,576)

Cuanto mayor es el nivel de confianza deseado, mayor será el tamaño de muestra necesario, ya que estamos exigiendo más certeza en los resultados. Estos valores provienen de la distribución normal estándar, lo que significa que, técnicamente, se puede elegir cualquier nivel de confianza, aunque los anteriores son los más habituales en la práctica.

Margen de error (E)

El margen de error expresa cuánto pueden desviarse los resultados de la muestra respecto al valor real en la población. Se expresa como un porcentaje. Por ejemplo, si el margen de error es del 5% y la encuesta indica que el 60% de las personas apoyan una medida, el valor real en la población estaría, con alta probabilidad, entre el 55% y el 65%.

Un margen de error más pequeño requiere un tamaño de muestra mayor, ya que se busca una mayor precisión en los resultados.

Proporción esperada (p)

La proporción esperada (también llamada proporción poblacional o proporción estimada) es el valor que se espera observar en la variable de interés. Por ejemplo, si queremos saber qué porcentaje de personas votará por un candidato y estimamos que será alrededor del 50%, entonces p = 0,5.

Cuando no se dispone de datos previos o históricos, se suele usar p = 0,5, ya que este valor maximiza la varianza y, por tanto, produce el tamaño de muestra más grande posible. Este enfoque se considera conservador porque garantiza que la muestra será suficientemente grande independientemente del resultado final.

Si se tiene una estimación más precisa (por ejemplo, p = 0,3), es posible utilizarla para reducir el tamaño necesario de la muestra, manteniendo la misma precisión y nivel de confianza.

Tamaño de la población (N)

El tamaño de la población se refiere al número total de personas a las que está dirigida la encuesta. En muchos casos, especialmente cuando la población es muy grande (por ejemplo, más de 100,000 personas), su influencia sobre el tamaño de la muestra es mínima. Sin embargo, cuando se trabaja con poblaciones pequeñas o medianas —como puede ser el caso de los clientes de una empresa (2,000 personas) o los habitantes de una ciudad pequeña (5,000 personas)— es esencial tener en cuenta este valor. Para ello, se debe aplicar una corrección estadística que ajuste el tamaño de la muestra calculado inicialmente, reflejando así la limitación impuesta por el tamaño finito de la población.

Cálculo para poblaciones grandes

Cuando la población objetivo es suficientemente grande, se puede utilizar la siguiente fórmula para estimar el tamaño de muestra requerido: n = \frac{Z^2 \cdot p \cdot (1 - p)}{E^2}, donde:

• n: tamaño de muestra requerido
• Z: valor z correspondiente al nivel de confianza deseado
• p: proporción estimada de individuos con la característica de interés
• E: margen de error tolerado (en forma decimal, por ejemplo, 0,05 para un 5%)

Esta fórmula proporciona una buena aproximación inicial cuando la población es lo suficientemente grande como para considerarse infinita en términos estadísticos.

Corrección para poblaciones finitas

Si la población tiene un tamaño limitado, es necesario ajustar el valor obtenido anteriormente mediante una corrección para poblaciones finitas. Esta corrección evita sobredimensionar la muestra y se calcula con la siguiente expresión: n_{corr} = \frac{n}{1 + \frac{n - 1}{N}}, donde:

• n_{corr}: tamaño de muestra ajustado
• n: tamaño de muestra calculado sin corrección
• N: tamaño total de la población

Aplicar esta corrección es especialmente importante cuando el tamaño de la población no es considerablemente mayor que el tamaño de muestra estimado, ya que garantiza una estimación más precisa y eficiente del tamaño muestral requerido.

Ejemplo práctico

Imaginemos que deseamos conocer la opinión de los ciudadanos de una ciudad con 20.000 habitantes sobre una nueva medida propuesta por el ayuntamiento. No contamos con datos previos sobre la proporción esperada de apoyo o rechazo, así que adoptamos un valor conservador de p = 0,5 (el valor que maximiza la varianza y, por tanto, el tamaño de muestra requerido). Queremos un nivel de confianza del 95 % y estamos dispuestos a aceptar un margen de error del 5 %.

Cálculo inicial usando la fórmula para poblaciones grandes

Usamos la fórmula general: n = \frac{Z^2 \cdot p \cdot (1 - p)}{E^2}.

Con los valores:

• Z = 1,96 (nivel de confianza del 95 %)
• p = 0,5
• E = 0,05

Sustituyendo: n = \frac{1,96^2 \cdot 0,5 \cdot (1 - 0,5)}{0,05^2} = \frac{3,8416 \cdot 0,25}{0,0025} = \frac{0,9604}{0,0025} = 384,16.

Es decir, si la población fuera muy grande (o infinita), necesitaríamos encuestar aproximadamente a 384 personas.

Aplicación de la corrección para población finita (N = 20.000)

Como en este caso la población total es conocida y no muy grande, conviene aplicar la corrección para poblaciones finitas: n_{corr} = \frac{n}{1 + \frac{n - 1}{N}} = \frac{384,16}{1 + \frac{384,16 - 1}{20000}} = \frac{384,16}{1 + 0,01916} \approx \frac{384,16}{1,01916} \approx 376,9.

Redondeando al número entero más cercano, sería suficiente con encuestar a 377 personas para mantener el mismo nivel de confianza y precisión. Es decir, gracias a la corrección, podemos reducir la muestra en unas 7 personas sin sacrificar calidad estadística.

Estimación de una media poblacional

Las fórmulas anteriores se utilizan para estimar proporciones (por ejemplo, el porcentaje de personas a favor o en contra de una medida). Sin embargo, si el objetivo es estimar un valor medio, como el ingreso mensual, el gasto en transporte o el número de horas de sueño, se utiliza una fórmula distinta.

Fórmula para estimar medias

La fórmula para calcular el tamaño de muestra cuando se desea estimar una media es: n = \frac{Z^2 \cdot \sigma^2}{E^2}, donde:

• n: tamaño de muestra requerido
• Z: valor z correspondiente al nivel de confianza deseado
• \sigma: desviación estándar esperada de la variable
• E: margen de error tolerado (en unidades de la variable)

Si no se conoce la desviación estándar de antemano, se puede:

• utilizar estimaciones de estudios previos,
• consultar datos históricos o fuentes oficiales, o
• realizar un estudio piloto para calcular una estimación preliminar.

Ejemplo para estimar una media

Supongamos que queremos conocer el ingreso mensual promedio de los habitantes de la misma ciudad (20,000 personas). De estudios anteriores, sabemos que la desviación estándar del gasto mensual ronda los 500 €. Queremos una estimación con 95 % de nivel de confianza y margen de error de ±50 €.

Entonces: n = \frac{1,96^2 \cdot 500^2}{50^2} = \frac{3,8416 \cdot 250000}{2500} = \frac{960400}{2500} = 384,16.

Aplicando la corrección para población finita: n_{corr} = \frac{384,16}{1 + \frac{384,16 - 1}{20000}} \approx \frac{384,16}{1,01916} \approx 376,9

Conclusión: Al igual que en el caso de proporciones, una muestra de 377 personas sería suficiente para estimar el ingreso medio con un error de ±50 €, siempre que la desviación estándar estimada sea razonablemente precisa.

Consideraciones adicionales

Al calcular el tamaño de la muestra para una encuesta, conviene tener en cuenta las siguientes recomendaciones:

• Si contamos con una estimación más precisa de la proporción esperada (por ejemplo, p = 0,2 o p = 0,8), el tamaño de la muestra requerido será menor que si utilizamos el valor conservador de 0,5.
• En encuestas con múltiples variables o preguntas, es aconsejable determinar el tamaño de la muestra en función del ítem más relevante o aquel que requiera mayor precisión.
• Es recomendable añadir un margen adicional al tamaño calculado para compensar posibles no respuestas, errores en la recolección de datos o encuestados que no cumplan los criterios de inclusión.
• El uso de técnicas de muestreo más complejas, como el muestreo estratificado o por conglomerados, puede afectar al tamaño de la muestra necesario y debe ser considerado en estudios avanzados.

Calculadora on-line del tamaño muestral

Para facilitar el cálculo del tamaño muestral de forma rápida y precisa, hemos desarrollado una aplicación en nuestro laboratorio. Esta herramienta ha sido diseñada pensando en la simplicidad de uso, al mismo tiempo que puede ser util para estudiantes y profesionales que necesiten realizar este tipo de estimaciones.

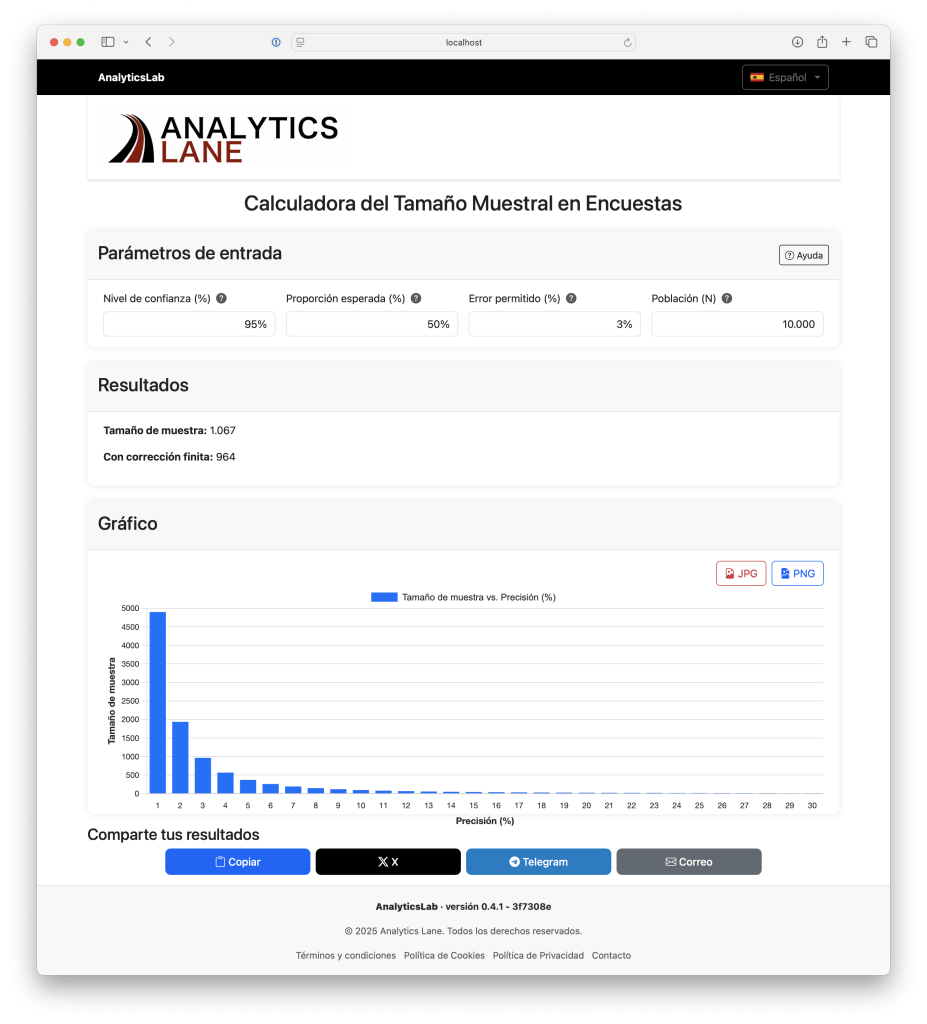
La aplicación permite introducir de manera intuitiva los parámetros clave del estudio: el nivel de confianza deseado, la proporción esperada de individuos que presentan la característica de interés y el margen de error aceptable. Además, ofrece la posibilidad de especificar el tamaño de la población total sobre la cual se desea realizar el estudio, lo que resulta especialmente útil en contextos con poblaciones finitas.

Una vez introducidos los datos, la aplicación calcula de forma instantánea el tamaño de muestra necesario tanto para una población infinita como para la población finita indicada (si se ha proporcionado). Esto permite comparar ambas estimaciones y tomar decisiones informadas según el contexto del estudio.

Como valor añadido, la herramienta genera automáticamente una gráfica que muestra cómo evoluciona el tamaño de la muestra en función de la proporción esperada. Esta visualización ayuda a comprender la sensibilidad del cálculo ante diferentes escenarios, y puede exportarse en varios formatos para incluirla fácilmente en informes, presentaciones o publicaciones.

Finalmente, la aplicación permite generar un enlace personalizado con los parámetros seleccionados, lo que facilita compartir los resultados o replicar los cálculos en cualquier momento desde cualquier dispositivo. Esto resulta especialmente útil para trabajo colaborativo o para documentación en proyectos más amplios.

Implementación en Python

A continuación, se presenta una implementación en Python de las fórmulas explicadas en esta entrada. Se incluyen dos funciones: una para el cálculo básico del tamaño de muestra para poblaciones infinitas y otra que aplica la corrección para poblaciones finitas si se proporciona el tamaño total de la población.

import math

def calcular_muestra(p, margen_error, z):
    """
    Calcula el tamaño de muestra para poblaciones grandes (infinitas).
    
    Parámetros:
    - p: proporción esperada (valor entre 0 y 1)
    - margen_error: margen de error tolerado (valor entre 0 y 1)
    - z: valor z correspondiente al nivel de confianza
    
    Retorna:
    - Tamaño de muestra calculado (entero redondeado hacia arriba)
    """
    q = 1 - p
    e = margen_error
    n0 = (z**2 * p * q) / (e**2)
    return math.ceil(n0)

def correccion_poblacion_finita(n0, N):
    """
    Aplica la corrección para poblaciones finitas al tamaño de muestra.
    
    Parámetros:
    - n0: tamaño de muestra calculado para población infinita
    - N: tamaño total de la población
    
    Retorna:
    - Tamaño de muestra corregido (entero redondeado hacia arriba)
    """
    n = (n0 * N) / (n0 + N - 1)
    return math.ceil(n)

def calcular_muestra_final(p, margen_error, z, N=None):
    """
    Calcula el tamaño de muestra, aplicando la corrección si se proporciona el tamaño poblacional.
    
    Parámetros:
    - p: proporción esperada (valor entre 0 y 1)
    - margen_error: margen de error tolerado (valor entre 0 y 1)
    - z: valor z correspondiente al nivel de confianza
    - N: (opcional) tamaño total de la población
    
    Retorna:
    - Tamaño de muestra final (entero)
    """
    n0 = calcular_muestra(p, margen_error, z)
    if N is not None:
        return correccion_poblacion_finita(n0, N)
    return n0

Un código que se puede usar de la siguiente manera:

# Parámetros del estudio
p = 0.5                # proporción esperada
margen_error = 0.05    # margen de error (5%)
z = 1.96               # valor z para 95% de nivel de confianza
N = 2000               # tamaño total de la población

# Cálculo con y sin corrección
n_sin_correccion = calcular_muestra(p, margen_error, z)
n_con_correccion = calcular_muestra_final(p, margen_error, z, N)

print(f"Tamaño de muestra (población infinita): {n_sin_correccion}")
print(f"Tamaño de muestra corregido (población finita N={N}): {n_con_correccion}")

Tamaño de muestra (población infinita): 385
Tamaño de muestra corregido (población finita N=2000): 323

Conclusiones

Determinar un tamaño de muestra adecuado es un paso esencial en el diseño de cualquier encuesta. Una muestra bien dimensionada garantiza que los resultados obtenidos sean estadísticamente válidos, precisos y representativos de la población objetivo. Comprender conceptos clave como el nivel de confianza, el margen de error, la proporción esperada y el tamaño de la población nos permite planificar estudios más robustos y tomar decisiones informadas desde el inicio del proceso de investigación.

Afortunadamente, calcular el tamaño de una muestra es relativamente sencillo gracias al código proporcionado en esta entrada o a la aplicación disponible en nuestro laboratorio.

Nota: La imagen de este artículo fue generada utilizando un modelo de inteligencia artificial.