
Imagínate en una sala con un grupo de personas, por ejemplo, en una oficina, un curso o una fiesta. Alguien dice: “Seguro que aquí dos personas cumplen años el mismo día”. ¿Te parece poco probable? La intuición nos hace pensar que, con 365 días que tienen un año, tendría que haber muchísimas personas en el grupo para que ocurra esta coincidencia.
Pero la estadística tiene otros planes: basta con 23 personas para que la probabilidad de coincidencia supere el 50%. Es decir, es más probable que ganar a cara o cruz. Y con solo 57 personas, esa probabilidad supera el 99%.
Este fenómeno se conoce como la Paradoja del Cumpleaños, y es un ejemplo fascinante de cómo nuestra intuición puede fallar estrepitosamente cuando se trata de probabilidades.
¿Cómo se calcula esa probabilidad?
Supongamos que en la sala hay 23 personas y que los cumpleaños están distribuidos aleatoriamente y de forma uniforme entre los 365 días del año (ignorando para el cálculo los años bisiestos y que la distribución real de nacimientos no es uniforme).
La forma más sencilla de calcular la probabilidad de que al menos dos personas compartan cumpleaños es usar el complemento:
Primero calculamos la probabilidad de que nadie comparta cumpleaños, y luego restamos a ese valor 1.
Cálculo de la probabilidad paso a paso
En base a esto, el proceso para obtener la probabilidad de que dos personas compartan cumpleaños seria:

- La primera persona puede cumplir años cualquier día del año → probabilidad = 365/365 = 1
- La segunda persona tiene 364 días disponibles para no coincidir con la primera → 364/365
- La tercera tiene 363 días para no coincidir con las dos anteriores → 363/365
- La cuarta, 362/365, y así sucesivamente…
La probabilidad de que no haya ninguna coincidencia entre 23 personas es: P(\text{ninguna coincidencia}) = \frac{365}{365} \times \frac{364}{365} \times \frac{363}{365} \times \cdots \times \frac{343}{365}
(La última fracción es 343/365 porque estamos considerando 23 personas, y se hacen 22 multiplicaciones desde la segunda persona en adelante).
El resultado de esa multiplicación es aproximadamente 0,4927, es decir, un 49,27% de probabilidad de que no haya coincidencias.
Y como nos interesa la probabilidad contraria —que sí haya al menos una coincidencia— simplemente restamos:P(\text{al menos una coincidencia}) = 1 - 0,4927 = \boxed{0,5073}
¡O sea, un 50,73% de probabilidad! Más de la mitad. Con solo 23 personas en la sala, es más probable que dos compartan cumpleaños que no.
¿Y si hay más personas?
Con 50 personas en la sala, la probabilidad de que al menos dos compartan cumpleaños es de aproximadamente 97%. Y con 57 personas, esa probabilidad supera ya el 99%.
La mejor forma de apreciar este fenómeno es a través de la siguiente gráfica donde se muestra cómo evoluciona esta probabilidad a medida que aumenta el número de personas en el grupo. La línea roja horizontal representa el umbral del 50% de probabilidad, mientras que la línea vertical amarilla indica el punto en el que se alcanza ese nivel: 23 personas. Este cruce muestra visualmente el sorprendente resultado de la paradoja del cumpleaños.
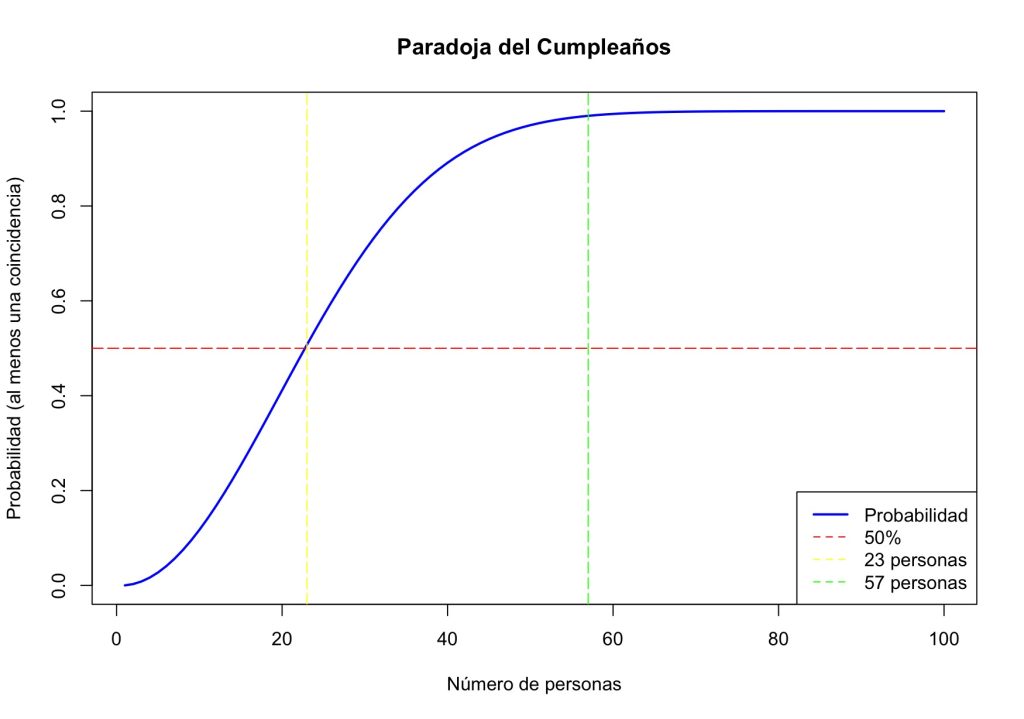
Además, la línea vertical verde señala el punto correspondiente a 57 personas, donde la curva de probabilidad se aproxima al 99%, prácticamente indistinguible del 100%.
¿Por qué es tan contraintuitivo el resultado?
El crecimiento tan abrupto que se ve en la gráfica es lo que hace que el resultado parezca paradójico. Nuestra intuición falla porque solemos pensar en las coincidencias con nosotros mismos, pero lo que realmente importa son todas las posibles parejas de personas en el grupo.
En un grupo de 23 personas, por ejemplo, hay 253 pares posibles de comparación. ¡Muchísimas oportunidades para que haya al menos una coincidencia!
¿Tiene alguna aplicación real la paradoja del cumpleaños?
Sí. Este principio no solo es una curiosidad teórica, también tiene aplicaciones:
- Criptografía: en ataques tipo “birthday attack”, donde se explotan colisiones en funciones hash.
- Pruebas aleatorias y simulaciones: para entender cómo aumentan las probabilidades de duplicidad en conjuntos aparentemente grandes.
Conclusión: ¿Es realmente una paradoja?
La llamada Paradoja del Cumpleaños no es una paradoja en el sentido matemático estricto, sino una paradoja de la intuición. Nos sorprende porque solemos subestimar cuántas comparaciones entre personas se pueden hacer en un grupo.
En realidad, el número de comparaciones posibles entre pares de personas crece muy rápido. En un grupo de n personas, hay: \frac{n(n-1)}{2} pares posibles. Por eso, incluso con grupos relativamente pequeños, el número de combinaciones crece lo suficiente como para que las coincidencias sean bastante probables.
Así que la próxima vez que estés en una reunión con 23 personas o más, no sería tan extraño que alguien diga: “¡Oye, yo también cumplo años ese día!”
Nota: La imagen de este artículo fue generada utilizando un modelo de inteligencia artificial.
Deja una respuesta