
Durante las últimas semanas he estado revisando algunas de las versiones de algoritmos UCB (Upper Confidence Bound) más utilizados a la hora de abordar problemas tipo Multi-Armed Bandit. Analizando durante este tiempo una importante cantidad de estos: UCB1, UCB2, UCB1-Tuned, UCB1-Normal, KL-UCB, UCB-V y CP-UCB. En esta ocasión vamos otro tipo de algoritmos como son los de seguimiento (pursuit algorithms), donde se define una política para la selección del bandido que se actualiza en cada una de las tiradas.
Algoritmos de seguimiento (pursuit algorithms)
Los algoritmos UCB se basan en estimar un nivel de confianza para la recompensa que se puede esperar de cada uno de los bandidos. Seleccionados el bandido para el cual su el intervalo de confianza máximo es mayor. A medida que aumenta el número de muestras los intervalos de confianza se hacen cada vez más estrechos, estando cada vez más seguros de seleccionar la jugada óptima en cada tirada. Una de las ventajas de estos algoritmos es que se pueden definir diferentes versiones en base a cómo calcula este nivel de confianza. A diferencia de UCB, los algoritmos de seguimiento (pursuit algorithms) mantienen una política explícita sobre cada uno de los bandidos, actualizando esta en base a los datos empíricos obtenidos.

Vamos a implementar un algoritmo de seguimiento que se describe en el excelente libro de Sutton y Barto. En este algoritmo el bandido con el que se juega en cada una de las tiradas se selecciona en base a una probabilidad que se asocia a cada uno de ellos. Inicialmente la probabilidad es exactamente la misma para todos los bandidos, el inverso del número de bandidos. Posteriormente, en cada una de las tiradas las probabilidades se actualizan en base a la siguiente expresión
p_i(t+1) = \begin{cases} p_i(t) + \beta (1 - p_i(t)) & \text{si } i = \arg \max_j \hat{X_j}\\ p_i(t) + \beta (0 - p_i(t)) & \text{otros} \\ \end{cases}donde \beta es un parámetro entre 0 y 1 que representa la tasa de aprendizaje.
Implementación en Python del algoritmo de seguimiento
Al igual que en ocasiones anteriores la implementación del algoritmo se puede acelerar utilizando la clase Epsilon implementada cuando se explico el método de valores iniciales optimistas. Para este algoritmo es necesario crear dos nuevas propiedades, una pública para guardar el parámetro \beta y una privada en la que se almacena la probabilidad de jugar con cada bandido. En esta ocasión también se tiene que actualizar el método run para actualizar la política después de cada una de las tiradas. Finalmente, como en todos los casos, se reemplaza el método select de la clase con el criterio de selección. Todo esto es lo que se muestra en el siguiente código.
class Pursuit(Epsilon):
def __init__(self, bandits, beta=0.01):
self.bandits = bandits
self.beta = beta
self.reset()
def run(self, episodes=1):
for i in range(episodes):
# Selección del bandido
bandit = self.select()
# Obtención de una nueva recompensa
reward = bandits[bandit].pull()
# Agregación de la recompensa al listado
self._rewards.append(reward)
# Actualización de la media
self._plays[bandit] += 1
self._mean[bandit] = (1 - 1.0/self._plays[bandit]) * self._mean[bandit] \
+ 1.0/self._plays[bandit] * reward
# Actualización de la probablidad
max_bandit = np.argmax(self._mean)
for i in range(len(self.bandits)):
if i == max_bandit:
self._p[i] += self.beta * (1 - self._p[i])
else:
self._p[i] -= self.beta * self._p[i]
return self.average_reward()
def select(self):
# Calculo de la probabilidad de seleccionar un bandido
prob = np.cumsum(self._p)
# Selección del bandido
return np.where(prob > np.random.random())[0][0]
def reset(self, initial=None):
self._rewards = []
self._plays = [0] * len(self.bandits)
self._mean = [0] * len(self.bandits)
self._p = [1 / len(self.bandits)] * len(self.bandits)Como se puede ver en el bandido se selecciona aleatoriamente, aunque, a medida que aumenta la experiencia, la probabilidad de seleccionar un bandido en concreto sea cercana a la unidad.
Evaluación de los resultados
Una vez se ha creado la clase para el algoritmo de seguimiento se puede comprobar cómo funciona este en comparación con UCB1. Como en ocasiones anteriores empleando para ello los bandidos basados en la distribución binomial. De este modo se puede hacer una comparación solamente con el siguiente código.
np.random.seed(0) bandits = [Bandit(0.02), Bandit(0.06), Bandit(0.10)] pursuit = Pursuit(bandits) ucb1 = UCB1(bandits) pursuit.run(200000) ucb1.run(200000) pursuit.plot(True, label='Pursuit') ucb1.plot(True, True, label='UCB1') plt.legend()
Obteniendo como resultado la siguiente figura.
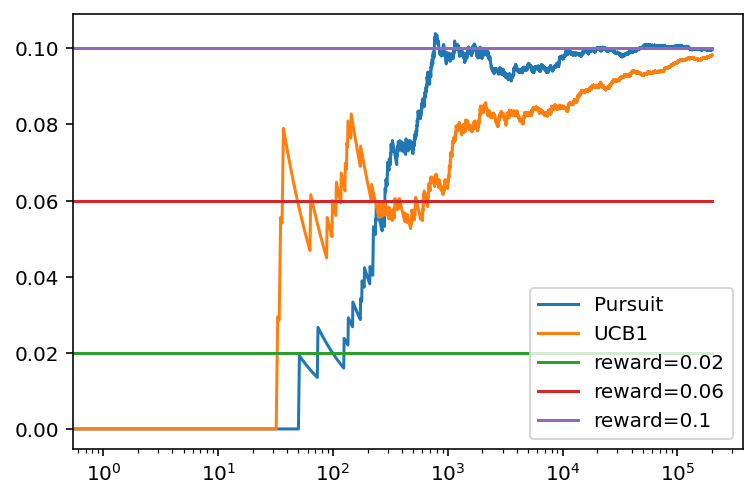
Unos resultados que son bastante buenos. Lo que se puede apreciar en el hecho de que la probabilidad de seleccionar al bandido óptimo al final del juego es cercana al 100%.
Importancia de la tasa de aprendizaje
En el ejemplo anterior, con un parámetro \beta igual a 0,01, los resultados son bastante buenos. Incluso converge más rápido que UCB1 a la recompensa óptima. Aunque hay que tener cuidado, ya que una mala elección de la tasa de aprendizaje puede hacer que se decida por un bandido que no sea el óptimo sin dar probabilidades a este de mejorar. Algo que se puede ver si se aumenta el parámetro solamente a 0,1 en la siguiente gráfica.

En donde al ejecutar con la tasa igual a 0,1 se puede ver que el algoritmo se queda rápidamente en un mínimo local que nos es el óptimo. Un efecto que no es el deseado. Aunque, este problema también no es exclusivo de este algoritmo, sino que puede afectar a otros de los que ya hemos visto.
Conclusiones
En esta ocasión hemos dejado de lado los algoritmos de la familia UCB para ver otros más básicos como es el de seguimiento (pursuit) que aún así ofrecen buenos resultados. Aunque para ello sea necesario prestar atención a la tasa de aprendizaje del algoritmo.
Deja una respuesta