Introducción a igraph en R (Parte 7): Centralidad de Bonacich

En el estudio de redes complejas, la centralidad es un concepto fundamental para entender la relevancia estructural de los nodos dentro de un sistema. En entregas anteriores de esta serie, hemos explorado medidas como la centralidad de autovector y la centralidad de Katz. En esta séptima parte, nos adentramos en la centralidad de Bonacich, una métrica que introduce la noción de poder relacional y dependencia estructural en una red.

A diferencia de otras métricas de centralidad que se centran únicamente en el número o la calidad de conexiones directas, la centralidad de Bonacich incorpora la influencia de los vecinos del nodo, ponderada por un parámetro que controla el nivel de dependencia respecto al entorno. Esta métrica, propuesta por el sociólogo Phillip Bonacich, es especialmente adecuada para analizar relaciones asimétricas de poder, donde la posición de un nodo depende tanto de su conectividad como de la posición que ocupan sus conexiones en la red.

Formulación de la centralidad de Bonacich

La centralidad de Bonacich se define matemáticamente mediante la siguiente expresión: C_B(i) = \sum_{j} (I - \beta A)^{-1}_{ij} \cdot \alpha, donde:

• A es la matriz de adyacencia de la red (puede ser ponderada o no),
• \beta es el parámetro de dependencia (determina cuánto importa la centralidad de los vecinos),
• \alpha es un parámetro de escala (puede interpretarse como una medida de influencia inicial),
• (I - \beta A)^{-1} es la matriz que incorpora las influencias indirectas en la red.

¿Cómo se interpreta el valor?

Un valor alto de centralidad de Bonacich indica que un nodo no solo está bien conectado, sino que está conectado con otros nodos que también tienen posiciones influyentes dentro de la red. En este sentido, el poder del nodo deriva del poder de sus conexiones.

En Analytics Lane

Curiosidad: La Ley de Twyman y la trampa de los datos “interesantes”

La centralidad de Bonacich es altamente dependiente del valor del parámetro de dependencia \beta:

• Cuando \beta > 0, la medida recompensa estar conectado a nodos influyentes, lo que permite modelar dinámicas de poder acumulativo. Este enfoque es útil cuando se quiere identificar actores que ganan influencia por estar bien posicionados en el núcleo de la red.
• Cuando \beta < 0, la medida penaliza estar conectado a nodos con alta centralidad, modelando una relación de dependencia o subordinación. Es decir, un nodo conectado a actores poderosos puede verse como débil o subordinado, reflejando situaciones como la dependencia de proveedores clave o subordinación en estructuras jerárquicas.
• Si \beta = 0, la centralidad de Bonacich se reduce a una forma de la centralidad de grado ponderada por \alpha.

En resumen:

• Valores positivos y altos implica nodo poderoso por asociación con otros poderosos.
• Valores negativos o bajos (con \beta < 0) implica nodo dependiente de otros más influyentes.
• Valores intermedios o neutros implica nodo con influencia moderada o equilibrada.

La elección de \beta < 0 permite modelar diferentes hipótesis sobre cómo circula el poder o la dependencia en la red, lo que convierte esta métrica en una herramienta flexible y poderosa para el análisis relacional.

Aplicaciones de la centralidad de Bonacich

La centralidad de Bonacich tiene múltiples aplicaciones en disciplinas como la sociología, la economía, la ciencia política y la ciencia de datos. Algunas de las áreas donde ha demostrado ser particularmente útil incluyen:

• Análisis de liderazgo y jerarquía organizacional: permite identificar actores con una posición estratégica de poder, incluso cuando no tienen el mayor número de conexiones directas.
• Estudios sobre difusión de información: al considerar las conexiones indirectas, ayuda a predecir el alcance de mensajes en redes sociales o de comunicación.
• Evaluación de influencia en mercados financieros: puede detectar agentes económicos cuyo poder emana de estar conectados con otros actores influyentes.
• Diagnóstico de resiliencia estructural: permite evaluar cómo la eliminación de ciertos nodos afecta la cohesión y distribución del poder en la red.
• Identificación de élites y concentración de poder: útil para estudiar fenómenos como la captura regulatoria o la influencia política desproporcionada.

Gracias a su formulación generalizable, esta métrica puede aplicarse tanto a redes homogéneas como heterogéneas, y adaptarse a distintos niveles de granularidad (por ejemplo, redes de individuos, organizaciones, países, etc.).

Cálculo y visualización de la centralidad de Bonacich con igraph

A modo de ejemplo, vamos a ver cómo calcular la centralidad de Bonacich con igraph en R utilizando una red simple. Para ello, podemos usar el siguiente código, que define la red y calcula la centralidad de Bonacich mediante la función bonpow().

library(igraph)

# Crear un grafo simple
g <- graph(edges = c(1,2, 1,3, 2,4, 2,5, 3,6, 5,6, 4,5, 3,4), directed = FALSE)

# Definir el parámetro de influencia
beta <- 0.2

# Calcular la centralidad de Bonacich (bonpow = Bonacich power centrality)
bonacich_centrality <- bonpow(g, exponent = beta)

# Mostrar los valores de centralidad
bonacich_centrality

Este código crea una red no dirigida con seis nodos conectados de forma específica y calcula la centralidad de Bonacich utilizando un valor de beta igual a 0.2. El resultado es un vector con los valores de centralidad para cada nodo:

0.762328 1.104691 1.036218 1.150339 1.104691 0.762328

En este caso, el cuarto nodo presenta el valor más alto de centralidad, lo que sugiere que está bien conectado y que sus vecinos también tienen un alto nivel de conectividad. Esto refuerza su posición estructural dentro de la red.

Visualización de la centralidad de Bonacich en el grafo

Para representar gráficamente la centralidad, podemos ajustar el tamaño de los nodos en función de sus valores y visualizar la red:

# Ajustar tamaños de los nodos según la centralidad de Bonacich
V(g)$size <- bonacich_centrality * 30

# Graficar el grafo
plot(g,
     vertex.label = round(bonacich_centrality, 3),
     edge.width = 2,
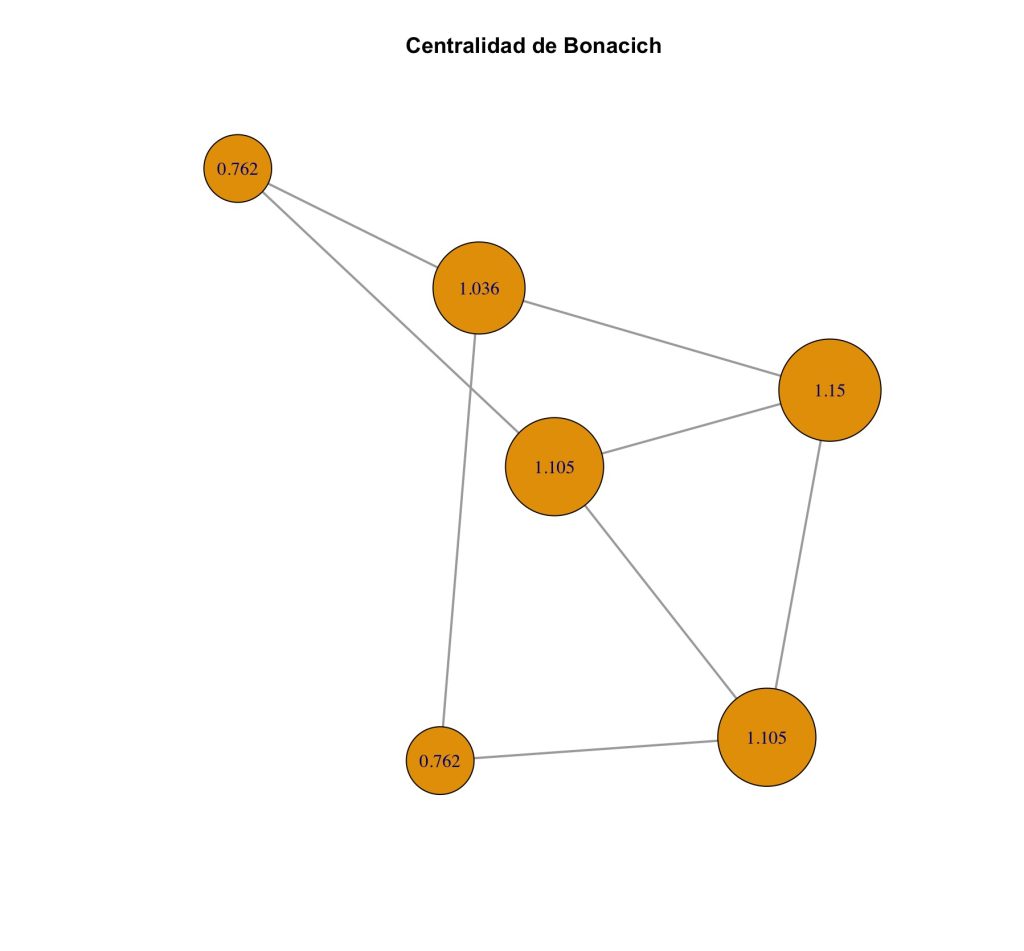
     main = "Centralidad de Bonacich")

Este código genera un grafo donde los nodos más grandes son los más influyentes según la centralidad de Bonacich. Los valores de centralidad se muestran como etiquetas numéricas sobre cada nodo, facilitando la interpretación del gráfico.

El grafo que se genera se puede ver en la siguiente figura.

Probar con diferentes valores de alpha

Uno de los aspectos más interesantes de la centralidad de Bonacich es cómo el parámetro beta afecta el cálculo. Este parámetro controla el grado en que la influencia de un nodo depende de la influencia de sus vecinos. Probar diferentes valores permite observar cómo cambian las posiciones relativas de los nodos según el nivel de dependencia e influencia que se modela.

A continuación, se muestra un ejemplo con varios valores de beta:

# Probar diferentes valores de beta
betas <- c(-0.3, 0, 0.3)

for (b in betas) {
  cat("\nBeta =", a, "\n")
  print(round(bonpow(g, exponent = b), 3))
}

Beta = 0.3 
[1] 0.528 1.191 1.390 0.821 1.191 0.528

Beta = 0.3 
[1] 0.739 1.108 1.108 1.108 1.108 0.739

Beta = 0.3 
[1] 0.766 1.109 1.006 1.164 1.109 0.766

Este código imprime los valores de centralidad de Bonacich para cada nodo con diferentes niveles de beta:

• Cuando beta es negativo, se penaliza estar conectado a nodos influyentes (se modela dependencia).
• Cuando beta es cero, la centralidad depende únicamente del grado del nodo (número de conexiones directas).
• Cuando beta es positivo, se recompensa estar conectado con nodos influyentes (se modela poder o prestigio).

Esta sensibilidad del modelo permite ajustar el análisis en función del contexto: por ejemplo, en redes donde el prestigio se transfiere por asociación (como redes académicas, políticas o sociales), valores positivos de beta pueden ser más adecuados. Por el contrario, en redes donde la dependencia de nodos centrales representa una debilidad (como en logística o infraestructuras críticas), valores negativos pueden resultar más informativos.

Visualización comparativa con diferentes valores de beta

También se puede crear una figura con los tres grafos para comparar visualmente el efecto de beta:

# Crear una disposición fija para que todos los grafos se vean iguales
layout_fixed <- layout_with_fr(g)

# Configurar la cuadrícula de gráficos
par(mfrow = c(3, 1), mar = c(1, 1, 3, 3)) 

# Graficar para cada valor de beta
for (b in betas) {
  # Calcular centralidad de Bonacich
  bc <- bonpow(g, exponent = b)
  
  # Ajustar el tamaño de los nodos proporcional a la centralidad
  V(g)$size <- bc * 30
  
  # Graficar
  plot(g,
       layout = layout_fixed,
       vertex.label = round(bc, 2),
       edge.width = 2,
       main = paste("β =", b),
       cex.main = 0.9) 
}

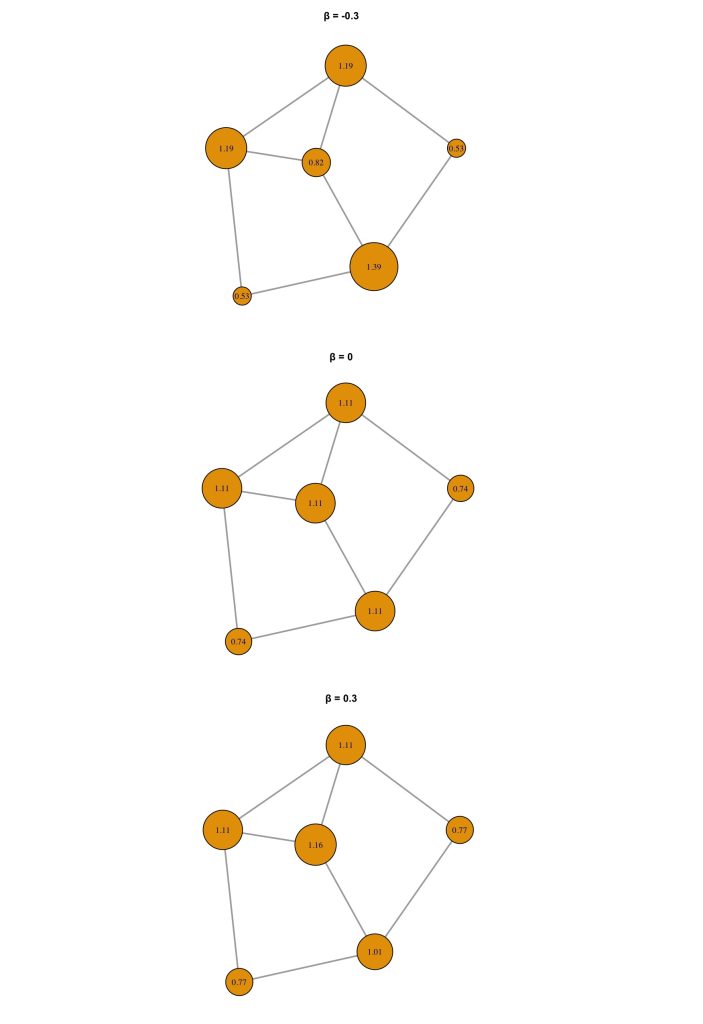
Al comparar los gráficos se puede apreciar los siguientes efectos:

• Los nodos más grandes son los más influyentes según la centralidad de Bonacich para ese valor de beta.
• Puedes observar cómo la estructura de poder e influencia cambia dependiendo del enfoque: dependencia, neutralidad o prestigio creciente.

Conclusiones

La centralidad de Bonacich es una métrica especialmente útil para analizar redes donde no basta con contar cuántas conexiones tiene un nodo, sino que resulta fundamental entender con quién está conectado. Esta perspectiva va más allá de las métricas tradicionales como el grado, la cercanía o la intermediación, introduciendo una dimensión de influencia o dependencia que puede ajustarse mediante el parámetro \beta.

A lo largo de este análisis, hemos visto que:

• Esta centralidad permite capturar estructuras jerárquicas y dinámicas de poder en una red, premiando o penalizando la conexión con nodos influyentes.
• El parámetro \beta juega un papel clave:
• Cuando \beta > 0, se premia estar conectado con nodos influyentes, modelando poder.
• Cuando \beta < 0, se penaliza esa conexión, modelando dependencia o vulnerabilidad.
• Cuando \beta = 0, la centralidad se reduce al grado tradicional.
• Visualmente, este enfoque permite detectar de forma intuitiva cuáles son los nodos con mayor peso estructural en función del contexto modelado.

En definitiva, la centralidad de Bonacich es una herramienta potente y flexible para estudiar redes en campos como la sociología, economía, ciencias políticas, comunicación o logística, donde comprender las relaciones de influencia es clave.

En la próxima entrega, profundizaremos precisamente en PageRank, una métrica derivada de la centralidad de eigenvector que revolucionó el análisis de redes con su aplicación en los motores de búsqueda.

Nota: La imagen de este artículo fue generada utilizando un modelo de inteligencia artificial.