Modelos BG/NBD para CLV

Uno de los conceptos clave en marketing para medir el valor del un cliente es el CLV. En entradas anteriores se ha visto la importancia del valor de vida de cliente y un modelo para obtener la tasa de retención. En los negocios en los que no existe una relación contractual, como puede ser una tienda on-line, identificar la probabilidad de que un cliente siga activo es clave. En la bibliografía existes múltiples modelos, para medir esta probabilidad y obtener así el CLV. En esta entrada se va a estudiar uno de los más utilizados, el modelo BG/NBD.

Inicialmente el modelo BG/NBD fue propuesto por Peter S. Fader et al. en el 2003 en este artículo. Este modelo fue desarrollado para describir el comportamiento de compra repetida en un entorno donde los clientes compran a un ritmo constante (aunque de manera estocástica) durante un período de tiempo, y luego se vuelven inactivos (abandonan).

El modelo BG/NBD 

Para la creación del modelo BG/NBD sus autores se han basado en las siguientes cinco suposiciones:

1. Mientras está activo, el número de transacciones realizadas por un cliente sigue un proceso de Poisson con tasa de transacción \lambda. Esto es equivalente a asumir que el tiempo entre transacciones se distribuye exponencial con la tasa de transacción \lambda, es decir, f(t_j | t_{j-1}; \lambda) = \lambda e^{-\lambda (t_j - t_{j-1})}
2. La heterogeneidad en \lambda sigue una distribución gamma con una función de densidad de probabilidad: f(\lambda | r, \alpha) = \frac{\alpha^r \lambda^{r-1} e^{\lambda - \alpha}}{\Gamma(r)}
3. Después de cualquier transacción, un cliente se vuelve inactivo con probabilidad p. Por lo tanto, el punto en el que el cliente “abandona” se distribuye a través de las transacciones de acuerdo con una distribución geométrica. De este modo, la probabilidad de abandono después de la transacción j es P_{inactivo}(j) = p (1-p)^{j-1}
4. La heterogeneidad en p sigue una distribución beta con función de densidad de probabilidad f(p|a,b) = \frac{p^{a-1} (1-p)^{b-1}}{B(a,b)}
5. La tasa de transacción \lambda y la probabilidad de deserción p varían independientemente entre los clientes.

Implementación en Python y R

El modelo BG/NBD se pueden encontrar implementado tanto en R como en Python. El modelo en R se puede encontrar en paquete BTYD (https://cran.r-project.org/web/packages/BTYD/index.html), mientras que en Python es en lifetimes (https://pypi.org/project/Lifetimes/). Para los ejemplos se utilizará al paquete de Python que se ha de instalar utilizando pip:

En Analytics Lane

Nuevo test de normalidad interactivo en el laboratorio de Analytics Lane

pip install lifetimes

Carga de los datos

Antes de trabajar con el modelo se ha de realizar una carga inicial de los datos en dónde se tiene tres características:

• Frecuencia: representa el número de compras repetidas que el cliente ha realizado. Esto significa que es uno menos que el número total de compras ya que la primera compra no se tiene en cuenta.
• T: representa la antigüedad del cliente en las unidades de tiempo elegidas (en el ejemplo semanas) y es igual al tiempo entre la primera compra y la finalización del periodo de observación
• Recencia: es la antigüedad del cliente cuando realizó su compra más reciente, en el caso de que el cliente realizase una única compra la recencia es igual a cero.

Esta tarea se puede realizar con el código:

from lifetimes.datasets import load_cdnow_summary
data = load_cdnow_summary(index_col = [0])

Ajuste del modelo BG/NBD

El ajuste del modelo se puede realizar utilizando el método BetaGeoFitter que se puede encontrar en la librería lifetimes de Phyton. Uno de los primeros resultados que se pueden obtener son el modelo son la gráfica de Frecuencia/Recencia en la que se representa el número de transacciones esperadas para un cliente en base a su recencia. 

from lifetimes import BetaGeoFitter
from lifetimes.plotting import plot_frequency_recency_matrix

bgf = BetaGeoFitter(penalizer_coef = 0.0)
bgf.fit(data['frequency'], data['recency'], data['T'])

plot_frequency_recency_matrix(bgf)

Obteniéndose la siguiente gráfica

Otro resultado interesante es la probabilidad de que un cliente siga vivo. Esto se puede ver en la matriz de probabilidad:

from lifetimes.plotting import plot_probability_alive_matrix
plot_probability_alive_matrix(bgf)

Con lo que se obtiene la siguiente gráfica

Una vez creado el modelo se pueden estimar las ventas esperadas para cada uno de los clientes en diferentes periodos de tiempo. Al seleccionar un cliente se puede obtener los siguientes valores.

for per in range(1, 10):
    print("Las ventas esperadas en", per, "periodos es", bgf.predict(per, 3, 30, 40))

A partir de lo que se puede observar por pantalla los siguientes resultados:

Las ventas esperadas en 1 periodos es 0.051478533257478386
Las ventas esperadas en 2 periodos es 0.10234426954917505
Las ventas esperadas en 3 periodos es 0.15261444751497685
Las ventas esperadas en 4 periodos es 0.2023055306896734
Las ventas esperadas en 5 periodos es 0.2514332555186299
Las ventas esperadas en 6 periodos es 0.3000126755884701
Las ventas esperadas en 7 periodos es 0.3480582024341811
Las ventas esperadas en 8 periodos es 0.39558364324353096
Las ventas esperadas en 9 periodos es 0.4426022357444098

Finalmente se puede comparar el modelo con los resultados obtenidos en la realidad.

from lifetimes.plotting import plot_period_transactions
plot_period_transactions(bgf)

De lo que se obtiene el siguiente resultado

Modelado con una histórico de transacciones

Normalmente el conjunto de datos disponibles es un histórico de transacciones y no de la forma que es requerida para la construcción de un modelo. En estos casos es necesario realizar una transformación de los datos al formato requerido. Para analizar los datos primero se ha de cargar un conjunto de transacciones: 

from lifetimes.datasets import load_transaction_data

transaction_data = load_transaction_data()

Posteriormente se ha de transformar utilizando el comando summary_data_from_transaction_data

from lifetimes.utils import summary_data_from_transaction_data

summary = summary_data_from_transaction_data(transaction_data, 'id', 'date', observation_period_end='2014-12-31')

Los datos ya transformado se pueden dividir el conjunto de datos en dos uno para el entrenamiento de los modelos y otro para la validación de estos. Esta es la forma para comprobar que el modelo implementado reproduce el comportamiento de los clientes en la realidad. Esto se puede realizar de la siguiente forma:

from lifetimes.utils import calibration_and_holdout_data

summary_cal_holdout = calibration_and_holdout_data(transaction_data, 'id', 'date', calibration_period_end = '2014-09-01', observation_period_end = '2014-12-31' )

A partir de este conjunto de datos, se puede realizar el ajuste utilizando las columnas terminadas en cal, y la prueba empleando las columnas terminadas en holdout:

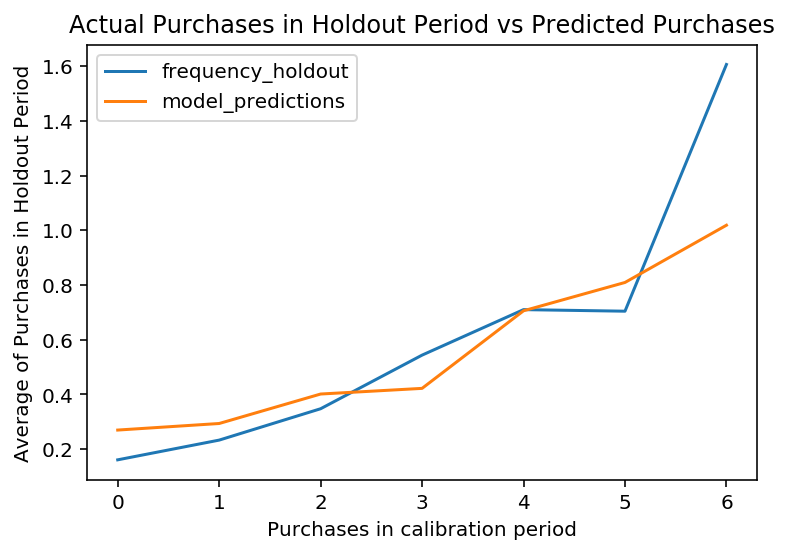
from lifetimes.plotting import plot_calibration_purchases_vs_holdout_purchases

bgf.fit(summary_cal_holdout['frequency_cal'], summary_cal_holdout['recency_cal'], summary_cal_holdout['T_cal'])
plot_calibration_purchases_vs_holdout_purchases(bgf, summary_cal_holdout)

Obteniéndose como resultado la siguiente gráfica

Conclusiones

En esta entrada se ha presentado el modelo BG/NBD para medir la probabilidad que un cliente continúe activo. Este modelo, cuando se verifican los supuestos, permite obtener una estimación de esta probabilidad. Así se puede obtener un valor clave para obtener el CLV de un cliente.