
La semana pasada hemos visto cómo resolver el problema del Bandido Multibrazo mediante un test A/B. Con el que se jugó con cada uno de los bandidos una cantidad de veces dada hasta que se estaba seguro de cuál era el mejor de los bandidos. Esta aproximación no es eficiente, ya que en muchos casos se puede saber rápidamente cuáles son los peores, por lo que se puede plantear otra estrategia más eficaz. Estrategia como Epsilon-Greedy en la que se selecciona el mejor hasta ese momento de los bandidos salvo un porcentaje de veces en las que se juega de forma aleatoria. Ocasiones con las que se explorar el resto de las soluciones.
Epsilon-Greedy
La estrategia Epsilon-Greedy es realmente sencilla. En esta, en primer lugar, se decide si se juega con el mejor bandido, aquel que ha devuelto la mayor recompensa promedio hasta el momento, o de forma completamente aleatoria. El porcentaje de veces en las que la estrategia jugará de forma aleatoria se seleccionará mediante un valor epsilon. Así se obtendrá la mejor recompensa con la información disponible, al mismo tiempo que es posible explorar otras soluciones con las tiradas aleatorias.
Esta simple estrategia permite maximizar la recompensa ya que jugará preferentemente con el bandido que ha ofrecido la mayor recompensa hasta ese momento. Sin tener que esperar a probar con cada uno de los bandidos la cantidad de veces que ha definido al principio.
Es importante tener en cuenta que si el valor de epsilon es bajo el algoritmo no podrá identificar rápidamente la mejor solución. Pero si el valor es alto, una vez identificada la mejor solución, se seguirá jugando una cantidad de veces elevada con una solución que no es la óptima. Por lo que el valor de epsilon es un compromiso que tiene que tener en cuenta tanto la exploración y la explotación.
Clase con la implementación del bandido
Para implementar esta estrategia se puede usar la clase bandido que se creó la semana pasada. Solamente que en esta ocasión es necesario contar con un atributo que nos indique la recompensa media histórica del bandido. Algo que se puede hacer con el método mean() de NumPy, aunque a medida que crece el número de jugadas esto puede no ser eficiente. Por lo que se puede actualizar el valor en cada una de las jugadas utilizando la siguiente fórmula
donde \overline{x_n} es la recompensa media del bandido que se ha obtenido en la tirada n y x_n es la recompensa obtenida en la tirada n. Lo que evita tener que calcular la media de vectores con miles de valores después de cada tirada.
Así se puede agregar dos atributos a la clase mean para almacenar la media y plays para almacenar el número de jugadas. Siendo ahora probability el atributo en el que almacena la probabilidad de que el bandido devuelva una recompensa. Lo que nos deja la clase Bandit de la siguiente forma.
import numpy as np
class Bandit:
"""
Implementación de un Bandido Multibrazo (Multi-Armed Bandit) basado
en una distribución binomial
Parameters
----------
probability : float
Probabilidad de que el objeto devuelva una recompensa
Attributes
----------
rewards : array
Históricos de recompensas generadas por el bandido
mean : float
Recompensa media histórica del bandido
plays : integer
Cantidad de veces que ha jugado con el bandido
Methods
-------
pull :
Realiza una tirada en el bandido
"""
def __init__(self, probability):
self.probability = probability
self.rewards = []
self.mean = 0
self.plays = 0
def pull(self):
# Obtención de una nueva recompensa
reward = np.random.binomial(1, self.probability)
# Agregación de la recompensa al listado
self.rewards.append(reward)
# Actualización de la media (es más rápido que usar la función media de la recompensa)
self.plays += 1
self.mean = (1 - 1.0/self.plays) * self.mean + 1.0/self.plays * reward
return rewardYa no es necesaria el atributo rewards, pero se puede dejar para usar poder seguir usando esta clase con el código de la semana pasada.
Implementación de la estrategia Epsilon-Greedy
Ahora que se ha actualizado la clase se puede implementar la estrategia. Para ello primero se tiene que decidir el porcentaje de veces que se jugará de forma aleatoria, por ejemplo, un 5%. Una vez hecho esto solamente se tiene que seleccionar un número aleatorio y en base a este seleccionar el bandido. Siendo la selección espilon veces de forma aleatoria y el resto de las veces seleccionando el que tiene la mejor recompensa hasta el momento.
Jugadas aleatorias
Para las jugadas en las que se seleccione aleatoriamente se puede usar el método numpy.random.choice(). Lo que devolverá un número al azar cada vez.
Seleccionar el mejor bandido
La primera idea para seleccionar el mejor bandido puede ser usar el método nunpy.argmax() de las medias. Aunque en este punto es importante tener en cuenta que los bandidos devuelven la recompensa con una frecuencia muy baja. Por lo que en las primeras jugadas todos tendrán una recompensa media igual a cero. Así, en caso de usar el método argmax con un vector de ceros, lo que tendremos en las primeras tiradas, devolverá siempre el primero, el cual puede que no sea el mejor.
Para solucionar este problema una opción puede ser seleccionar aleatoriamente uno de los bandidos en caso de que exista un empate entre ellos. Lo que ayudará a explorar más rápidamente las opciones al principio. Para lo que se puede combatir el uso de numpy.where() para identificar las posición de los bandidos con el valor máximo y numpy.random.choice(), para seleccionar uno de estos.
Así se pude crear la siguiente implementación para resolver el problema.
np.random.seed(0)
bandits = [Bandit(0.02), Bandit(0.04), Bandit(0.06), Bandit(0.08), Bandit(0.10)]
evaluations = 8500
eps = 0.05
rewards = []
for i in range(evaluations):
p = np.random.random()
if p < eps:
j = np.random.choice(len(bandits))
else:
means = [b.mean for b in bandits]
max_bandits = np.where(means == np.max(means))[0]
j = np.random.choice(max_bandits)
rewards.append(bandits[j].pull())
total_reward = np.sum([np.sum(bandit.rewards) for bandit in bandits])
avg_reward = total_reward / evaluationsResultados
De cara a comparar con la solución obtenida la semana pasada con un test A/B en primer lugar vamos a ver cómo funciona el algoritmo con 8500 jugadas. En este caso se obtiene una recompensa media de 9.6%, bastante superior al 8,1% que se observó la semana pasada con el test A/B. Además, se puede comprobar la evolución de la recompensa media, para lo que se puede imprimir la recompensa media en cada jugada. Lo que se puede obtener con el siguiente código.
import matplotlib.pyplot as plt cumulative_average = np.cumsum(rewards) / (np.arange(len(rewards)) + 1) plt.plot(range(len(rewards)), cumulative_average)
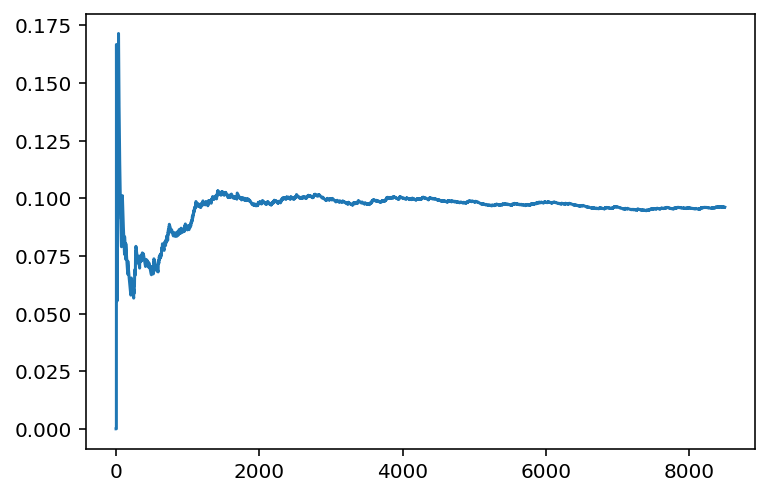
Lo que muestra que, en torno a las 1000 jugadas, la recompensa media obtenida ya se acerca a la final. Lo que indica que en este punto el algoritmo se ha decidido por jugar mayoritariamente con el bandido que ofrece una recompensa del 10%. Una conclusión a la que se ha llegado bastante más rápido que mediante el uso del test A/B.
En las primeras jugadas se puede ver una recompensa promedio por encima del máximo, pero es algo que puede suceder debido a la aleatoriedad de las recompensas. Aunque esto se corrige rápidamente a medida que aumentan el número de jugadas.
Posiblemente en torno a las 1000 jugadas ya no sea necesario explorar otros resultados. Pero el algoritmo seguirá jugando un 5% de las veces aleatoriamente, algo que veremos la semana que viene cómo se puede mejorar.
Conclusiones
Hoy hemos visto cómo solucionar un problema de Bandido Multibrazo utilizando para ello la estrategia de Epsilon-Greedy. Una estrategia que es sencilla de implementar y ofrece buenos resultados. La próxima semana veremos cómo mejorar el algoritmo para evitar que siga jugando aleatoriamente cuando ya se ha decidido por un bandido.






Deja una respuesta