
Las anomalías, también conocidas como ”outliers”, son puntos que se desvían significativamente de la mayoría de los otros puntos en un conjunto de datos. Por lo que saber detectarlas es una tarea clave en múltiples aplicaciones. Empezando por la seguridad informática, donde los ataques tienen un patrón diferente al uso legítimo de los recursos, hasta en mantenimiento predictivo, donde una anomalía puede anticipar un fallo inminente. En esta entrada se analizará uno de los métodos más efectivos para la detección de anomalías: el Histogram-Based Outlier Score (HBOS). Un algoritmo, que como su nombre indica, se basa en el uso de histogramas.
Tabla de contenidos
Fundamentos de Histogram-Based Outlier Score (HBOS)
Histogram-Based Outlier Score (HBOS) es un algoritmo de detección de anomalías que se basa en la creación de histogramas. Asignando un puntaje de anomalía en función de la rareza de cada punto. Para lo que se basa en la premisa de que las anomalías son puntos menos frecuentes que los normales. A través de la construcción de histogramas, HBOS identifica estas discrepancias de frecuencia y asigna puntajes de anomalía en función de la rareza de cada punto de datos.
HBOS usa los siguiente tres pasos para obtener el índice de rareza de cada uno de los puntos de un conjunto de datos
1. División en bins
El primer paso en el proceso de HBOS es dividir el espacio de características en una serie de ”bins” o contenedores. Representado cada uno de estos “bins” regiones discretas del espacio de características fundamentales para la construcción de los histogramas. La cantidad de “bins” se puede fijar por el usuarios o determinar en base a algún algoritmo (como pueden ser la regla de Sturges o la regla de Rice).

2. Construcción de los histogramas
Una vez que el espacio de características se ha dividido en “bins”, se construye un histograma para cada una de las características del conjunto de datos. Cada histograma mide la frecuencia de ocurrencia de los puntos en cada bin. Con lo que se obtiene una representación visual de la distribución de los datos para cada característica.
3. Cálculo del puntaje de anomalía
Una vez que se han construido los histogramas, HBOS calcula el puntaje de anomalía para cada punto del conjunto de datos. Puntaje que se determina en base a la frecuencia observada en cada uno de los ”bins”. Para lo que se toma el valor de cada bin en el que cae el punto, normalizando en relación con la anchura de estos y la cantidad total de puntos en el conjunto de datos. Los puntos de datos que caen en ”bins” con una menor frecuencia tendrán puntajes de anomalía más altos.
Ventajas de HBOS
En comparación con otros algoritmos de detección de anomalías, HBOS cuenta con las siguiente:
- Simplicidad y eficiencia: HBOS es un algoritmo relativamente simple y eficiente en comparación con otros métodos. Debido a su enfoque basado en la construcción de histogramas, HBOS evita la necesidad de ajustar modelos probabilísticos complejos o la selección de parámetros complicados. Esto lo hace más fácil de implementar, entender y computacionalmente eficiente, especialmente para conjuntos de datos grandes o de alta dimensionalidad.
- Independencia de la distribución: HBOS no hace suposiciones específicas sobre la distribución subyacente de los datos, a diferencia de algunos otros métodos como Elliptic Envelope y One-Class SVM, que asumen distribuciones específicas como la gaussiana. Esto significa que HBOS puede funcionar bien en una variedad más amplia de conjuntos de datos con diferentes tipos de distribuciones, lo que lo hace más versátil.
- Eficiente con datos de alta dimensionalidad: HBOS es particularmente útil para conjuntos de datos de alta dimensionalidad. A causa de su eficiencia computacional. A diferencia de métodos como LOF y One-Class SVM, que pueden volverse computacionalmente costosos a medida que aumenta el número de dimisiones debido a la necesidad de calcular las distancias en el espacio de características. HBOS utiliza histogramas para calcular los puntajes de anomalía, lo que lo hace más rápido y eficiente.
Sin embargo, es importante tener en cuenta que no hay un algoritmo que sea óptimo para todos los escenarios. La efectividad de HBOS en relación con otros métodos dependerá en cada caso de las características de los conjuntos de datos específicos de cada problema.
Hiperparámetros importantes en HBOS
Los hiperparámetros más importantes de HBOS son:
- Número de Bins: Este parámetro determina cuántos ”bins” se utilizan para dividir el espacio de características. Un número demasiado bajo puede resultar en una pérdida de información, mientras que un número demasiado alto puede aumentar el tiempo de computación.
- Contaminación: Este parámetro define la proporción de puntos de datos que se consideran anomalías en el conjunto de datos. Un valor más alto significa que se considerarán más puntos como anomalías.
Uso de HBOS en Python
Actualmente HBOS no está implementado en Scikit-learn, pero si existe una implementación en la librería PyOD. Una librería de Python especializada en algoritmos de detección de anomalías. Como es habitual se puede instalar a través de pip escribiendo el siguiente comando:
pip install pyod
Alternativamente también se puede instalar a través de conda con el siguiente comando:
conda install -c conda-forge pyod
Una vez instalado PyOD ya se puede usar HBOS, y otros algoritmos para detectar anomalías.
Creación de un conjunto de datos de ejemplo
En primer lugar, es necesario contar con un conjunto de datos con anomalías para utilizar HBOS. Para lo que se puede crear un conjunto de datos al que se agrega ruido. El conjunto de datos que se va a usar se creará con el siguiente código.
import numpy as np
import matplotlib.pyplot as plt
# Generar datos normales
np.random.seed(42)
data_norm1 = np.random.normal(loc=0, scale=1, size=(1000, 2))
data_norm2 = np.random.normal(loc=5, scale=1, size=(1000, 2))
# Generar anomalías con distribución diferente
anomalies = np.random.normal(loc=10, scale=2, size=(50, 2))
# Combinar datos normales y anomalías
X = np.vstack([data_norm1, data_norm2, anomalies])
# Visualizar los datos
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], s=10)
plt.title("Conjunto de Datos con Anomalías")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()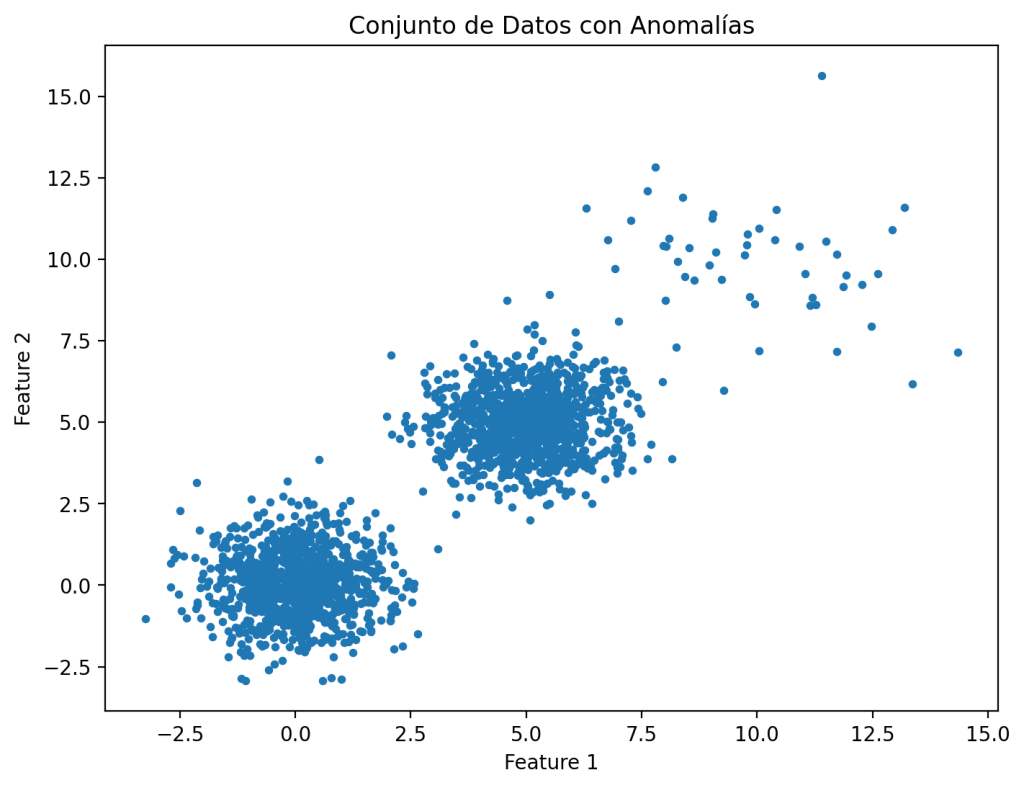
HBOS, a pesar de no realizar suposiciones sobre la distribución subyacente de los datos, funciona mejor en conjuntos de datos donde las anomalías siguen una distribución diferente a la normal. En este ejemplo, se han generado dos grupos de datos normales con distribuciones normales diferentes y añadido algunas anomalías que siguen una tercera distribución. Este es un escenario común en los datos de muchas aplicaciones reales.
Creación de un modelo
Una vez se dispone de los datos, solamente hay que entrenar el modelo indicando la contaminación (el porcentaje de datos anómalos que se esperan en el conjunto de datos). Para los que se usa el método fit() de una instancia de HBOS. A partir de esto, se pueden obtener las puntuaciones de anomalía para todos los puntos con el método decision_function() y una predicción con el método predict(). En el siguiente ejemplo se crea un gráfico donde los puntos anómalos se colorean en rojo.
from pyod.models.hbos import HBOS
# Inicializar y ajustar el modelo HBOS
hbos_model = HBOS(contamination=0.1)
hbos_model.fit(X)
# Obtener las puntuaciones de anomalía
anomaly_scores = hbos_model.decision_function(X)
# Etiquetar los puntos de datos como anomalías o no anomalías
labels = hbos_model.predict(X)
# Visualizar el conjunto de datos con las anomalías detectadas
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='coolwarm', s=10)
plt.title("Conjunto de Datos con Anomalías Detectadas (HBOS)")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()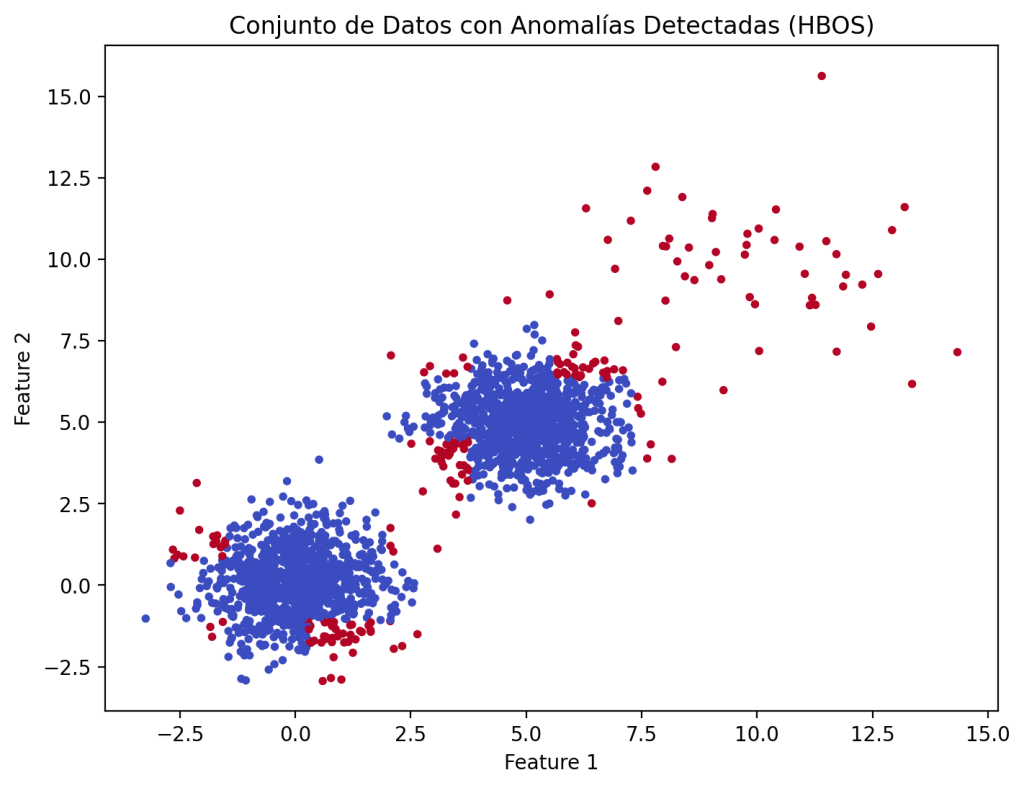
En la gráfica se puede ver claramente que el algoritmo detecta correctamente las anomalías que se han agregado al conjunto de datos. Hay algunos datos normales que se identifican como anomalías, pero esto se puede solucionar reduciendo el valor de la contaminación. La contaminación, al fijar el porcentaje de anomalías en el conjunto de datos, define el punto umbral a partir del cual un dato se marca como anómalos o no.
Conclusiones
HBOS utiliza la información de los histogramas para evaluar la rareza de los puntos en relación con los datos normales. Siendo un algoritmo cuyas bases son fáciles de entender. Este enfoque simple pero efectivo hace que HBOS sea una herramienta ampliamente utilizada en la detección de anomalías.
Deja una respuesta